You are a prisoner sentenced to death. The Emperor offers you a chance to live by playing a simple game. He gives you 50 black marbles, 50 white marbles and 2 empty bowls. He then says, "Divide these 100 marbles into these 2 bowls. You can divide them any way you like as long as you use all the marbles. Then I will blindfold you and mix the bowls around. You then can choose one bowl and remove ONE marble. If the marble is WHITE you will live, but if the marble is BLACK... you will die."
How do you divide the marbles up so that you have the greatest probability of choosing a WHITE marble?
Hint
The answer does not guarantee 100% you will chose a white marble, but you have a much better chance.
Answer
Place 1 white marble in one bowl, and place the rest of the marbles in the other bowl (49 whites, and 50 blacks).
This way you begin with a 50/50 chance of choosing the bowl with just one white marble, therefore life! BUT even if you choose the other bowl, you still have ALMOST a 50/50 chance at picking one of the 49 white marbles.
"You can punch a hole in an apple using a straw. How do you think that makes your milkshake feel..???" Start Solving It...
Friday, March 11, 2011
Einstien,Newton,Jamse watt & You..Where are You ??
You find yourself half way between Tokyo and Rio de Janeiro; about as far from Mexico City as from Moscow.
Albert Einstein waits to the left, ready to explain his theory of relativity. A short distance to your right James Watt hopes to recount his development of the steam engine to you. John Steinbeck and Isaac Bashevis Singer crouch over you, vying for your attention.
Your surroundings are conventional and functional. One aspect stands out: A piece of furniture - represented in 2 or 3 specimens in the typical home - recurs here hundreds of times.
What is this piece of furniture, and where are you?
Albert Einstein waits to the left, ready to explain his theory of relativity. A short distance to your right James Watt hopes to recount his development of the steam engine to you. John Steinbeck and Isaac Bashevis Singer crouch over you, vying for your attention.
Your surroundings are conventional and functional. One aspect stands out: A piece of furniture - represented in 2 or 3 specimens in the typical home - recurs here hundreds of times.
What is this piece of furniture, and where are you?
You find yourself half way between Tokyo and Rio de Janeiro; about as far from Mexico City as from Moscow.
Albert Einstein waits to the left, ready to explain his theory of relativity. A short distance to your right James Watt hopes to recount his development of the steam engine to you. John Steinbeck and Isaac Bashevis Singer crouch over you, vying for your attention.
Your surroundings are conventional and functional. One aspect stands out: A piece of furniture - represented in 2 or 3 specimens in the typical home - recurs here hundreds of times.
What is this piece of furniture, and where are you?
Albert Einstein waits to the left, ready to explain his theory of relativity. A short distance to your right James Watt hopes to recount his development of the steam engine to you. John Steinbeck and Isaac Bashevis Singer crouch over you, vying for your attention.
Your surroundings are conventional and functional. One aspect stands out: A piece of furniture - represented in 2 or 3 specimens in the typical home - recurs here hundreds of times.
What is this piece of furniture, and where are you?
Thursday, March 10, 2011
Which Tringle is Larger the Other
How can this be true???? All the lines are straight, the shapes that make up the top picture are the same as the ones in the bottom picture so where does the gap come from????
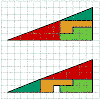
If you can't see the solution by looking you could try printing it out and looking along the edges....
Failing that then let me just tell you the answer....
The green triangle has dimensions 2 x 5 and gradient 2 / 5 = 0.4
The red triangle has dimensions 3 x 8 and gradient 3 / 8 = 0.375
 Hence the gradient of the green triangle is greater than that of the red triangle.
Hence the gradient of the green triangle is greater than that of the red triangle.
An exaggerated outline might look like....
answer triangle puzzle missing square
In summary the missing square in the bottom triangle is made up for by the fact that it's hypotenuse bends out where as for the top triangle it bends in.
Source : http://puzzles.nigelcoldwell.co.uk/twenty.htm

If you can't see the solution by looking you could try printing it out and looking along the edges....
Failing that then let me just tell you the answer....
The green triangle has dimensions 2 x 5 and gradient 2 / 5 = 0.4
The red triangle has dimensions 3 x 8 and gradient 3 / 8 = 0.375
 Hence the gradient of the green triangle is greater than that of the red triangle.
Hence the gradient of the green triangle is greater than that of the red triangle.An exaggerated outline might look like....
answer triangle puzzle missing square
In summary the missing square in the bottom triangle is made up for by the fact that it's hypotenuse bends out where as for the top triangle it bends in.
Source : http://puzzles.nigelcoldwell.co.uk/twenty.htm
Two Creepers Climbing a Tree
Two creepers, one jasmin and other rose, are both climbing up and round a cylindrical tree trunk. jasmine twists clockwise and rose anticlockwise, both start at the same point on the ground. before they reach the first branch of the tree the jasmine had made 5 complete twists and the rose 3 twists. not counting the bottom and the top, how many times do they cross?
The first thing to realise is the vertical aspect of the puzzle is something of an illusion. For convenience we will proceed as if they both travel vertically at the same speed and thus complete the journey in the same unspecified time Ttotal, but this is for convenience regardless of the times the path described is the same.
From here we may now consider their motion as being constrained to the outer edge of a circle in the horizontal plane. The problem now becomes not dissimilar to a puzzle involving the overlap of the hands of a clock, though of course the hands are moving in opposite directions.
Each of the creepers will have speeds 5w and 3w. Where 'w' is some unspecified angular velocity in degrees per second, although the units are arbitrary. Using speed is distance over time or time = distance / speed, knowing that the total distance travelled 360 degrees times 5 revolutions or 3 revolutions we can easily show Ttotal as a function of w. Ttotal = 360 * 5 / (5w) or Ttotal = 360 * 3 / (3w) hence Ttotal = 360 / w. We will need this later.
The First Coincidence
We now have two motions around a circle starting at one point, travelling in opposite directions, with speeds 3w and 5w. We need to solve this for time.
jasmine and rose creepers puzzle
Ama

We know a total distance of 360 degrees is travelled by two objects with speeds 5w and 3w. Our equations of motion give us:
360=5wt + 3wt = 8wt
t = 360 / 8w
So our first overlap is at t = 360 / 8w. In terms of subsequent overlaps the puzzle is in some ways reset. They are co-existent at this time and travelling in opposite directions. if we were to calculate the next time of overlap it would be the same. We now know an overlap occurs every 360 / 8w
Total Coincidence
An overlap occurs every 360 / 8w for a time of Ttotal = 360 / w hence the number of coincidence is
Ttotal / time between coincidence
(360 / w) / (360 / 8w)
8
since the division is exact we know that the last coincidence is at t = Ttotal, hence there are 7 overlaps not including the top and bottom.
Source : puzzles.nigelcoldwell.co.uk/thirtytwo.htm
The first thing to realise is the vertical aspect of the puzzle is something of an illusion. For convenience we will proceed as if they both travel vertically at the same speed and thus complete the journey in the same unspecified time Ttotal, but this is for convenience regardless of the times the path described is the same.
From here we may now consider their motion as being constrained to the outer edge of a circle in the horizontal plane. The problem now becomes not dissimilar to a puzzle involving the overlap of the hands of a clock, though of course the hands are moving in opposite directions.
Each of the creepers will have speeds 5w and 3w. Where 'w' is some unspecified angular velocity in degrees per second, although the units are arbitrary. Using speed is distance over time or time = distance / speed, knowing that the total distance travelled 360 degrees times 5 revolutions or 3 revolutions we can easily show Ttotal as a function of w. Ttotal = 360 * 5 / (5w) or Ttotal = 360 * 3 / (3w) hence Ttotal = 360 / w. We will need this later.
The First Coincidence
We now have two motions around a circle starting at one point, travelling in opposite directions, with speeds 3w and 5w. We need to solve this for time.
jasmine and rose creepers puzzle
Ama

We know a total distance of 360 degrees is travelled by two objects with speeds 5w and 3w. Our equations of motion give us:
360=5wt + 3wt = 8wt
t = 360 / 8w
So our first overlap is at t = 360 / 8w. In terms of subsequent overlaps the puzzle is in some ways reset. They are co-existent at this time and travelling in opposite directions. if we were to calculate the next time of overlap it would be the same. We now know an overlap occurs every 360 / 8w
Total Coincidence
An overlap occurs every 360 / 8w for a time of Ttotal = 360 / w hence the number of coincidence is
Ttotal / time between coincidence
(360 / w) / (360 / 8w)
8
since the division is exact we know that the last coincidence is at t = Ttotal, hence there are 7 overlaps not including the top and bottom.
Source : puzzles.nigelcoldwell.co.uk/thirtytwo.htm
Labels:
Adobe Puzzle,
Amazon,
Amazon Puzzle,
Google Puzzle,
Microsoft Puzzle
Stupid Puzzle But Makes you Stuck..Missing 1 Dollar
This puzzle gets e-mailed to me all the time and i don't really like it because it's less of a lateral thinnking riddle than a bit of a trick. Plus I've always struggled to find a good way of explaining it....
3 men go into a hotel missing dollar
You possibly wont be surprised to hear that there is no missing dollar. It adds up just fine. In tring to explain this I've always thought it was helpful to consider the puzzle with some different numbers in it. (Equally it may not be helpful, you could skip to the end.) Consider this....
3 men go into a hotel.
The man behind the desk said the room is $3000 so each man paid $1000 and went to the room.
A while later the man behind the desk realized the room was only $25 (he's that stupid,) so he sent the bellboy to the 3 guys' room with $2975.
On the way the bellboy couldn't figure out how to split $2975 evenly between 3 men, so he gave each man a $991 and kept the other $2 for himself.
Now at this point you would never ask:
This meant that the 3 men each paid $9 for the room, which is a total of $27 add the $2 that the bellboy kept = $29. Where is the other $2971?
Remember this puzzle is exactly the same. it's just the numbers from the first puzzle are confusing (to me anyway.) In this we know there is no missing $2971 because we saw where all that money went. By making this number larger we can see it moving, we can see that it was mostly shared by the three men. In the real puzzle there are several small amounts bobbing about and they're harder to track. But the answer is the same, there is no more a missing dollar than there was a missing $2971.
So the short answer:
There is no missing dollar. The men spent $27. Of which $25 went on the room and $2 went to the light fingered bell boy. You can not add the $2 the bellboy has to the $27 the men spent as this $2 actually comes out of the $27 the men spent, the other $25 going on the room.
Put another way consider how the $30 breaks down:
* $25 - room
* $3 (3x $1) back to the men
* $2 Bellboy
Source : puzzles.nigelcoldwell.co.uk/twentyeight.htm
3 men go into a hotel missing dollar
You possibly wont be surprised to hear that there is no missing dollar. It adds up just fine. In tring to explain this I've always thought it was helpful to consider the puzzle with some different numbers in it. (Equally it may not be helpful, you could skip to the end.) Consider this....
3 men go into a hotel.
The man behind the desk said the room is $3000 so each man paid $1000 and went to the room.
A while later the man behind the desk realized the room was only $25 (he's that stupid,) so he sent the bellboy to the 3 guys' room with $2975.
On the way the bellboy couldn't figure out how to split $2975 evenly between 3 men, so he gave each man a $991 and kept the other $2 for himself.
Now at this point you would never ask:
This meant that the 3 men each paid $9 for the room, which is a total of $27 add the $2 that the bellboy kept = $29. Where is the other $2971?
Remember this puzzle is exactly the same. it's just the numbers from the first puzzle are confusing (to me anyway.) In this we know there is no missing $2971 because we saw where all that money went. By making this number larger we can see it moving, we can see that it was mostly shared by the three men. In the real puzzle there are several small amounts bobbing about and they're harder to track. But the answer is the same, there is no more a missing dollar than there was a missing $2971.
So the short answer:
There is no missing dollar. The men spent $27. Of which $25 went on the room and $2 went to the light fingered bell boy. You can not add the $2 the bellboy has to the $27 the men spent as this $2 actually comes out of the $27 the men spent, the other $25 going on the room.
Put another way consider how the $30 breaks down:
* $25 - room
* $3 (3x $1) back to the men
* $2 Bellboy
Source : puzzles.nigelcoldwell.co.uk/twentyeight.htm
Consider a standard chess board. What is the diameter of the largest circle that can be drawn on the board whilst only drawing on the black squares.
The circle could fit entirely with in one black square, it could be like the green circle below, but we want the biggest, and that is the red circle:-

There is some logic as to why this is the largest circle that can be drawn. It has to do with the fact that a circle can only intercept a straight line at two points, you can visualise a square around our red circle travelling through the corners in the same place. (you could calculate the dimensions of this too.)
Using the yellow triangle we can easily calculate the radius and therefore the diameter of the circle. We need the hypotenuse of a triangle with opposite and adjacent sides of 1.5 and 0.5
Radius^2 = 1.5^2 + 0.5^2
Radius^2 = 10/4
Radius = Sqrt(10) / 2
Diameter = Sqrt(10) = 3.1623
Source : puzzles.nigelcoldwell.co.uk/thirtyonehint.htm

There is some logic as to why this is the largest circle that can be drawn. It has to do with the fact that a circle can only intercept a straight line at two points, you can visualise a square around our red circle travelling through the corners in the same place. (you could calculate the dimensions of this too.)
Using the yellow triangle we can easily calculate the radius and therefore the diameter of the circle. We need the hypotenuse of a triangle with opposite and adjacent sides of 1.5 and 0.5
Radius^2 = 1.5^2 + 0.5^2
Radius^2 = 10/4
Radius = Sqrt(10) / 2
Diameter = Sqrt(10) = 3.1623
Source : puzzles.nigelcoldwell.co.uk/thirtyonehint.htm
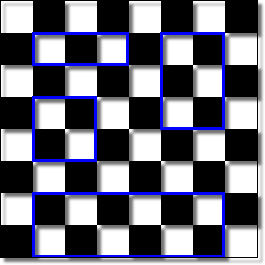
How many squares are there on a chessboard?? (the answer is not 64) Can you extend your technique to calculate the number of rectangles on a chessbrd

All the red squares in the above picture would count as valid squares, so we are asking how many squares of any dimension from 1x1 to 8x8 there are on a chess board.
The key is to think how many positions there are that each size of square can be located...
A 2x2 square, for example, can be located in 7 loactions horizontally and 7 locations vertically. ie in 49 different positions. Consider the table below...
size horizontal positions vertical positions positons
1x1 8 8 64
2x2 7 7 49
3x3 6 6 36
4x4 5 5 25
5x5 4 4 16
6x6 3 3 9
7x7 2 2 4
8x8 1 1 1
total 204
There is a formula for the sum of squares of the integers
1^2 + 2^2 + 3^2 + ... + n^2
n(n+1)(2n+1)
Sum = ------------
6
In our case, with n = 8, this formula gives 8 x 9 x 17/6 = 204.
In total there are 204 positions. this is the sum of the number of possible positions for all the different sized squares.
Can you extend your technique to calculate the number of rectangles on a chessboard?
Below are some examples of possible rectangles...
All of the above examples would be vailid rectanges...
The key to this problem is to think of each rectangle individually and consider the number of positions it can be located. For example a 3x7 rectangle can be located in 6 positions horizontally and 2 vertically. From this we can build a matrix of all the possible rectangles and sum.
dimesions 1 2 3 4 5 6 7 8
positions 8 7 6 5 4 3 2 1
1 8 64 56 48 40 32 24 16 8
2 7 56 49 42 35 28 21 14 7
3 6 48 42 36 30 24 18 12 6
4 5 40 35 30 25 20 15 10 5
5 4 32 28 24 20 16 12 8 4
6 3 24 21 18 15 12 9 6 3
7 2 16 14 12 10 8 6 4 2
8 1 8 7 6 5 4 3 2 1
1296
In total then there are 1296 possible rectangles.
More Explaination
There are 64 one-by-one squares,
49 two-by-two squares, ...
(8-n)^2 n-by-n squares, ...
1 eight-by-eight square;
2 x (7x8) one-by-two rectangles,
2 x (6x8) one-by-three rectangles, ...
2 x (1x8) one-by-eight rectangles;
2 x (6x7) two-by-three rectangles, ...
2 x (1x7) two-by-eight rectangles; ...;
2 x (1x2) seven-by-eight rectangles.
This can all be simplified to find the sum total as the sum of the
cubes of integers 1 to 8, which is 8^2 x 9^2 / 4 or 36^2 = 1296.
Count the rectangles by rows.
In row 1 there are n 1 by 1s , n-1 1 by 2s, ... two 1 by n-1s and
one 1 by n. Row Total =
n + (n-1) + (n-2) + ... + 3 + 2 + 1 = n(n+1)/2 rectangles.
But of course there are n rows, giving n (row sum).
Now count all rectangles of height 2. Start in the bottom row. There are
n 2 by 1s and n-1 2 by 2s and ... and one 2 by n. Row Total =
n + (n-1) + (n-2) + ... + 3 + 2 + 1 = n (n+1)/2
The row total is the same, as it will be for all the rectangles of height
3, 4, ... n because they all share the same bases at the bottom of the
board. However, there are only n-1 rows of height 2 and n-2 rows of
height 3 etc. Thus,
number 1 by any totals: n [n(n+1)/2]
number 2 by any totals: (n-1) [n(n+1)/2]
number 3 by any totals: (n-2) [n(n+1)/2]
...
number n by any totals: 1 [n(n+1)/2]
So the total number of rectangles is [n(n+1)/2](n + n-1) + ... + 3+ 2+1)
or Total = [n(n+1)/2]^2
which,is the sum of the cubes from 1 to n.
Source : puzzles.nigelcoldwell.co.uk/twentyseven.htm
Wednesday, March 9, 2011
Odd Ball & Weighing System Puzzle ..A Good Puzzle
You have 12 balls with you out of which one ball is either lighter or heavier than the rest of the balls which are of the same weight. You have a weighing scale with you and are allowed to use it three times. How can you find out which ball is the odd one and also if it is lighter or heavier than the rest?
Number the balls 1 to 12. Weigh 1, 2, 3, and 4 against 5, 6, 7, and 8.
If (1, 2, 3, 4) and (5, 6, 7, 8) balance:
Weigh 9 and 10 against 11 and 8 (we know 8 is not the odd ball).
If (9, 10) and (11, 8) balance: then 12 is the odd one.
Weigh 12 against any other to find out if it is heavy or light.
If (9, 10) and (11, 8) do not balance: suppose 11 and 8 are heavier,
than 9 and 10; then either 11 is heavy, or 9 is light, or 10 is light.
Weigh 9 against 10; if they balance, 11 is heavy; if they do not,
the lighter of 9 and 10 is the odd ball.
(Similar argument if 11 and 8 are lighter than 9 and 10).
If (1, 2, 3, 4) and (5, 6, 7, 8) do not balance:
Suppose 5, 6, 7, and 8 are heavier than 1, 2, 3, & 4. Then: one of
(1, 2, 3, or 4) is light, or else one of (5, 6, 7, or 8) is heavy.
Weigh 1, 2, and 5 against 3, 6, and 9.
If they balance: then either 7 is heavy, or 8 is heavy, or 4 is light.
Weigh 7 against 8; if they balance, 4 is the odd ball, otherwise the
heavier of 7 and 8 is the odd ball.
If (1, 2, 5) and (3, 6, 9) do not balance: suppose 1, 2, and 5 are lighter
than 3, 6, and 9; then either 6 is heavy, or 1 is light, or 2 is light.
Weigh 1 against 2 to find out which one of the three choices is true.
Otherwise, suppose 1, 2, and 5 are heavier than 3, 6, and 9; then either 3
is light, or 5 is heavy.
Weigh 3 against (say) 2 to find out which of the two choices is true.
(Similar argument if 1, 2, and 5 are lighter than 3, 6, and 9).
Number the balls 1 to 12. Weigh 1, 2, 3, and 4 against 5, 6, 7, and 8.
If (1, 2, 3, 4) and (5, 6, 7, 8) balance:
Weigh 9 and 10 against 11 and 8 (we know 8 is not the odd ball).
If (9, 10) and (11, 8) balance: then 12 is the odd one.
Weigh 12 against any other to find out if it is heavy or light.
If (9, 10) and (11, 8) do not balance: suppose 11 and 8 are heavier,
than 9 and 10; then either 11 is heavy, or 9 is light, or 10 is light.
Weigh 9 against 10; if they balance, 11 is heavy; if they do not,
the lighter of 9 and 10 is the odd ball.
(Similar argument if 11 and 8 are lighter than 9 and 10).
If (1, 2, 3, 4) and (5, 6, 7, 8) do not balance:
Suppose 5, 6, 7, and 8 are heavier than 1, 2, 3, & 4. Then: one of
(1, 2, 3, or 4) is light, or else one of (5, 6, 7, or 8) is heavy.
Weigh 1, 2, and 5 against 3, 6, and 9.
If they balance: then either 7 is heavy, or 8 is heavy, or 4 is light.
Weigh 7 against 8; if they balance, 4 is the odd ball, otherwise the
heavier of 7 and 8 is the odd ball.
If (1, 2, 5) and (3, 6, 9) do not balance: suppose 1, 2, and 5 are lighter
than 3, 6, and 9; then either 6 is heavy, or 1 is light, or 2 is light.
Weigh 1 against 2 to find out which one of the three choices is true.
Otherwise, suppose 1, 2, and 5 are heavier than 3, 6, and 9; then either 3
is light, or 5 is heavy.
Weigh 3 against (say) 2 to find out which of the two choices is true.
(Similar argument if 1, 2, and 5 are lighter than 3, 6, and 9).
Labels:
Amazon Puzzle,
Google Puzzle,
Microsoft Puzzle,
rosoft Puzzle
Tuesday, March 8, 2011
If the probability of observing a car in 30 minutes on a highway is 0.95- Google Asked It
If the probability of observing a car in 30 minutes on a highway is 0.95, what is the probability of observing a car in 10 minutes (assuming constant default probability)?
1st Way
Let p is a probability to see a car in 10 minutes.
Then (1-p) is probability NOT to see a car in 10 minutes.
Then probability NOT to see a car in 30 minutes is (1-p)*(1-p)*(1-p).
(1-p)^3 == 0.05
So p = 1-0.05^(1/3)~ 0.63
2nd Way
You have to look at your probability of NOT seeing a car, which is .05 in 30 minutes. In order to break this down into 10 minute chunks, you need to figure out how you arrived at that probability, which would be x * x * x = .05, so x ^ 3 = .05.
1st Way
Let p is a probability to see a car in 10 minutes.
Then (1-p) is probability NOT to see a car in 10 minutes.
Then probability NOT to see a car in 30 minutes is (1-p)*(1-p)*(1-p).
(1-p)^3 == 0.05
So p = 1-0.05^(1/3)~ 0.63
2nd Way
You have to look at your probability of NOT seeing a car, which is .05 in 30 minutes. In order to break this down into 10 minute chunks, you need to figure out how you arrived at that probability, which would be x * x * x = .05, so x ^ 3 = .05.
Sunday, March 6, 2011
Chess Puzzle
You have a chessboard (8×8) plus a big box of dominoes (each 2×1). I use a marker pen to put an “X” in the squares at coordinates (1, 1) and (8, 8) - a pair of diagonally opposing corners. Is it possible to cover the remaining 62 squares using the dominoes without any of them sticking out over the edge of the board and without any of them overlapping? You cannot let the dominoes stand on their ends.
The nature of this problem is such that if you can't find a hook you'll be thinking about it for ever.
Firstly the answer to this question is NO you can't cover the board. There is a trick here, look at the board below.

Do you notice anything about the squares at 1,1 and 8,8? Well they are both the same colour.
If you think about a Domino placed any where on the board it will necessarily cover a black square and a white square. We have in our example a 32 black squares and 30 white squares to cover. So it just can't be done.
Source : puzzles.nigelcoldwell.co.uk/sixteen.htm
The nature of this problem is such that if you can't find a hook you'll be thinking about it for ever.
Firstly the answer to this question is NO you can't cover the board. There is a trick here, look at the board below.

Do you notice anything about the squares at 1,1 and 8,8? Well they are both the same colour.
If you think about a Domino placed any where on the board it will necessarily cover a black square and a white square. We have in our example a 32 black squares and 30 white squares to cover. So it just can't be done.
Source : puzzles.nigelcoldwell.co.uk/sixteen.htm
What Colore of My Hat..??
Inside of a dark closet are five hats: three blue and two red. Knowing this, three smart men go into the closet, and each selects a hat in the dark and places it unseen upon his head.
Once outside the closet, no man can see his own hat. The first man looks at the other two, thinks, and says, “I cannot tell what color my hat is.” The second man hears this, looks at the other two, and says, “I cannot tell what color my hat is either.” The third man is blind. The blind man says, “Well, I know what color my hat is.” What color is his hat?
We will call the people A, B & C in the order that they speak.
A does not know what colour hat he is wearing. A would only know what colour hat he was wearing if he could see that B & C were both wearing red hats, (as there were only two red hats in the cupboard.) This is not the case so either:-
B & C are both wearing blue hats
OR
one of B & C is wearing red and the other is wearing blue
When B speaks we obviously assume he has thought of all of this. When B looks at C if C were wearing red then he would know that he must be wearing blue as they can't both be wearing red. But this does not happen so C must be wearing blue, meaning that B doesn't know if he is wearing red or blue:
The third person must be wearing a BLUE hat
Source : puzzles.nigelcoldwell.co.uk/twelve.htm
Once outside the closet, no man can see his own hat. The first man looks at the other two, thinks, and says, “I cannot tell what color my hat is.” The second man hears this, looks at the other two, and says, “I cannot tell what color my hat is either.” The third man is blind. The blind man says, “Well, I know what color my hat is.” What color is his hat?
We will call the people A, B & C in the order that they speak.
A does not know what colour hat he is wearing. A would only know what colour hat he was wearing if he could see that B & C were both wearing red hats, (as there were only two red hats in the cupboard.) This is not the case so either:-
B & C are both wearing blue hats
OR
one of B & C is wearing red and the other is wearing blue
When B speaks we obviously assume he has thought of all of this. When B looks at C if C were wearing red then he would know that he must be wearing blue as they can't both be wearing red. But this does not happen so C must be wearing blue, meaning that B doesn't know if he is wearing red or blue:
The third person must be wearing a BLUE hat
Source : puzzles.nigelcoldwell.co.uk/twelve.htm
Without knowing the combination numbers, what is the maximum number of trials required to open the safe ..Combination Problem
You are to open a safe without knowing the combination. Beginning with the dial set at zero, the dial must be turned counter-clockwise to the first combination number, (then clockwise back to zero), and clockwise to the second combination number, (then counter-clockwise back to zero), and counter-clockwise again to the third and final number, where upon the door shall immediately spring open. There are 40 numbers on the dial, including the zero.
Without knowing the combination numbers, what is the maximum number of trials required to open the safe (one trial equals one attempt to dial a full three-number combination)?
Well clearly the answer is not 40x40x40 = 64000, that would just be too easy, not so much a lateral thinking puzzle as just a sum.
The key word here is 'immediately.' The implication of this is that you do not have to try 40 times at the last number for each combination of the first number two numbers.
With this in mind you see that after any combination of the first two numbers you can, instead of trying all of the 40 possibilities for the last number, just turn the dial all the way to the end for the last number; in doing this you will necessarily pass the correct number where upon 'the door shall immediately spring open.'
If that hasn't cleared it up the answer is below:-
40 x 40 = 1600
Source : puzzles.nigelcoldwell.co.uk/elevenhint.htm
Without knowing the combination numbers, what is the maximum number of trials required to open the safe (one trial equals one attempt to dial a full three-number combination)?
Well clearly the answer is not 40x40x40 = 64000, that would just be too easy, not so much a lateral thinking puzzle as just a sum.
The key word here is 'immediately.' The implication of this is that you do not have to try 40 times at the last number for each combination of the first number two numbers.
With this in mind you see that after any combination of the first two numbers you can, instead of trying all of the 40 possibilities for the last number, just turn the dial all the way to the end for the last number; in doing this you will necessarily pass the correct number where upon 'the door shall immediately spring open.'
If that hasn't cleared it up the answer is below:-
40 x 40 = 1600
Source : puzzles.nigelcoldwell.co.uk/elevenhint.htm
Who Cheated The Wife
In a certain matriarchal town, the women all believe in an old prophecy that says there will come a time when a stranger will visit the town and announce whether any of the men folks are cheating on their wives. The stranger will simply say “yes” or “no”, without announcing the number of men implicated or their identities. If the stranger arrives and makes his announcement, the women know that they must follow a particular rule: If on any day following the stranger’s announcement a woman deduces that her husband is not faithful to her, she must kick him out into the street at 10 A.M. the next day. This action is immediately observable by every resident in the town. It is well known that each wife is already observant enough to know whether any man (except her own husband) is cheating on his wife. However, no woman can reveal that information to any other. A cheating husband is also assumed to remain silent about his infidelity.
The time comes, and a stranger arrives. He announces that there are cheating men in the town. On the morning of the 10th day following the stranger’s arrival, some unfaithful men are kicked out into the street for the first time. How many of them are there?
One cheating husband:
If only one man were cheating then clearly his wife would work this out on the first day as she would have known that no other husbands were cheating and so the cheating husband must be hers.
Two cheating husbands:
Consider this from the point of view of Bettie one of the wives (Bettie and Anna) who are being cheated on, though all their positions are infact the same. Bettie would be aware that Anna's husband was cheating on her and would therefore expect that she would deduce this on the first day as in the example above, because this does not happen Bettie knows that Anna is also aware of a cheating husband. Since Betty was not aware of this it must be her husband who is cheating. Anna will go through the same thought process and so two men will be thrown out on the 2nd day.
Three cheating husbands:
Charlotte will be aware Anna and Bettie's cheating husbands and expect the process to be solved as in the example above on the 2nd day, when this doesn't happen she will know that Anna and Bettie must also be aware of 2 cheating husbands and will hence chuck out her fella on the third day. Anna and Betty will think and do the same.
N cheating husbands:
Any of the wives being cheated on will be aware of N-1 cheating husbands and expect the process to be solved on the (N-1)th day, when this doesn't happen they all become aware that all the other wives that they thought were being cheated were all under the same impression and hence they must be the Nth cheated on wife. Hence on the Nth day N wives throw out N husbands.
Source : http://puzzles.nigelcoldwell.co.uk/nine.htm
The time comes, and a stranger arrives. He announces that there are cheating men in the town. On the morning of the 10th day following the stranger’s arrival, some unfaithful men are kicked out into the street for the first time. How many of them are there?
One cheating husband:
If only one man were cheating then clearly his wife would work this out on the first day as she would have known that no other husbands were cheating and so the cheating husband must be hers.
Two cheating husbands:
Consider this from the point of view of Bettie one of the wives (Bettie and Anna) who are being cheated on, though all their positions are infact the same. Bettie would be aware that Anna's husband was cheating on her and would therefore expect that she would deduce this on the first day as in the example above, because this does not happen Bettie knows that Anna is also aware of a cheating husband. Since Betty was not aware of this it must be her husband who is cheating. Anna will go through the same thought process and so two men will be thrown out on the 2nd day.
Three cheating husbands:
Charlotte will be aware Anna and Bettie's cheating husbands and expect the process to be solved as in the example above on the 2nd day, when this doesn't happen she will know that Anna and Bettie must also be aware of 2 cheating husbands and will hence chuck out her fella on the third day. Anna and Betty will think and do the same.
N cheating husbands:
Any of the wives being cheated on will be aware of N-1 cheating husbands and expect the process to be solved on the (N-1)th day, when this doesn't happen they all become aware that all the other wives that they thought were being cheated were all under the same impression and hence they must be the Nth cheated on wife. Hence on the Nth day N wives throw out N husbands.
Source : http://puzzles.nigelcoldwell.co.uk/nine.htm
Which Switch control The Bulbs
A windowless room contains three identical light fixtures, each containing an identical light bulb. Each light is connected to one of three switches outside of the room. Each bulb is switched off at present. You are outside the room, and the door is closed. You have one , and only one, opportunity to flip any of the external switches. After this, you can go into the room and look at the lights, but you may not touch the switches again. How can you tell which switch goes to which light?
The consensus of opinion seems to be this:
Switch on switch number 1, wait a few minutes and switch on switch number 2.
Enter the room and which ever bulb is on and is hot is connected to switch 1, whichever is on and cold is connected to switch number 2, and the remaining bulb is connected to switch number 3.
Source : puzzles.nigelcoldwell.co.uk/six.htm
The consensus of opinion seems to be this:
Switch on switch number 1, wait a few minutes and switch on switch number 2.
Enter the room and which ever bulb is on and is hot is connected to switch 1, whichever is on and cold is connected to switch number 2, and the remaining bulb is connected to switch number 3.
Source : puzzles.nigelcoldwell.co.uk/six.htm
Light Bulbs Puzzle
There are 100 light bulbs lined up in a row in a long room. Each bulb has its own switch and is currently switched off. The room has an entry door and an exit door. There are 100 people lined up outside the entry door. Each bulb is numbered consecutively from 1 to 100. So is each person.
Person No. 1 enters the room, switches on every bulb, and exits. Person No. 2 enters and flips the switch on every second bulb (turning off bulbs 2, 4, 6, …). Person No. 3 enters and flips the switch on every third bulb (changing the state on bulbs 3, 6, 9, …). This continues until all 100 people have passed through the room.
What is the final state of bulb No. 64? And how many of the light bulbs are illuminated after the 100th person has passed through the room?
Right first the answers: Light Bulb 64 is on. The total number of bulbs which are on including #64 is 10.
The working:-
There is a more eloquent way of working this but first lets look at a more brute force technique i used an Excel spread sheet:-
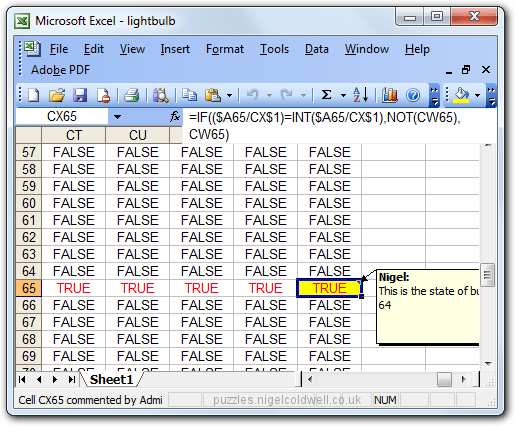
excel light switch puzzle
I'll just briefly explain to you the function used:
=IF(($A65/CX$1)=INT($A65/CX$1),NOT(CW65),CW65)
The 'if' command checks to see if the bulb number divided the person number is an integer that is to say it does the calculation twice (bulb number / person number) and rounds off one of the calculations to the nearest integer. It then compares the unrounded number to the rounded one. If these are the same then the person is entitled to switch that light bulb. Eg: Person 5 is entitled to switch bulb 50 but not 51, do the sum if you like.
I have included the Spread sheet, you will need Winzip and Excel to view the file:
lightbulb.zip - 46.9KB
A More eloquent approach.
First think who will operate each bulb, obviously person #2 will do all the even numbers, and say person #10 will operate all the bulbs that end in a zero. So who would operate for example bulb 48:
Persons numbered: 1 & 48, 2 & 24, 3 & 16, 4 & 12, 6 & 8 ........
That is all the factors (numbers by which 48 is divisible) will be in pairs. This means that for every person who switches a bulb on there will be someone to switch it off. This willl result in the bulb being back at it's original state.
So why aren't all the bulbs off?
Think of bulb 36:-
The factors are: 1 & 36, 2 & 13, 6 & 6
Well in this case whilst all the factors are in pairs the number 6 is paired with it's self. Clearly the sixth person will only flick the bulb once and so the pairs don't cancel. This is true of all the square numbers.
There are 10 square numbers between 1 and 100 (1, 4, 9, 16, 25, 36, 49, 64, 81 & 100) hence 10 bulbs remain on.
source : http://puzzles.nigelcoldwell.co.uk/six.htm
Person No. 1 enters the room, switches on every bulb, and exits. Person No. 2 enters and flips the switch on every second bulb (turning off bulbs 2, 4, 6, …). Person No. 3 enters and flips the switch on every third bulb (changing the state on bulbs 3, 6, 9, …). This continues until all 100 people have passed through the room.
What is the final state of bulb No. 64? And how many of the light bulbs are illuminated after the 100th person has passed through the room?
Right first the answers: Light Bulb 64 is on. The total number of bulbs which are on including #64 is 10.
The working:-
There is a more eloquent way of working this but first lets look at a more brute force technique i used an Excel spread sheet:-

excel light switch puzzle
I'll just briefly explain to you the function used:
=IF(($A65/CX$1)=INT($A65/CX$1),NOT(CW65),CW65)
The 'if' command checks to see if the bulb number divided the person number is an integer that is to say it does the calculation twice (bulb number / person number) and rounds off one of the calculations to the nearest integer. It then compares the unrounded number to the rounded one. If these are the same then the person is entitled to switch that light bulb. Eg: Person 5 is entitled to switch bulb 50 but not 51, do the sum if you like.
I have included the Spread sheet, you will need Winzip and Excel to view the file:
lightbulb.zip - 46.9KB
A More eloquent approach.
First think who will operate each bulb, obviously person #2 will do all the even numbers, and say person #10 will operate all the bulbs that end in a zero. So who would operate for example bulb 48:
Persons numbered: 1 & 48, 2 & 24, 3 & 16, 4 & 12, 6 & 8 ........
That is all the factors (numbers by which 48 is divisible) will be in pairs. This means that for every person who switches a bulb on there will be someone to switch it off. This willl result in the bulb being back at it's original state.
So why aren't all the bulbs off?
Think of bulb 36:-
The factors are: 1 & 36, 2 & 13, 6 & 6
Well in this case whilst all the factors are in pairs the number 6 is paired with it's self. Clearly the sixth person will only flick the bulb once and so the pairs don't cancel. This is true of all the square numbers.
There are 10 square numbers between 1 and 100 (1, 4, 9, 16, 25, 36, 49, 64, 81 & 100) hence 10 bulbs remain on.
source : http://puzzles.nigelcoldwell.co.uk/six.htm
City , People & Childrem Until A Boy Born
A mythical city contains 100,000 married couples but no children. Each family wishes to “continue the male line”, but they do not wish to over-populate. So, each family has one baby per annum until the arrival of the first boy. For example, if (at some future date) a family has five children, then it must be either that they are all girls, and another child is planned, or that there are four girls and one boy, and no more children are planned. Assume that children are equally likely to be born male or female.
Let p(t) be the percentage of children that are male at the end of year t. How is this percentage expected to evolve through time?
I worked this little riddle out for myself also so it's probably fairly easy...
Right unusually let me tell you the answer first:-
p(t) ≠ f(t) p(t) = 50%
That is to say the percentage of children that are male is not a function of time and is always 50%. This may seem a little counter intuitive as we know that at some point in time a family could conceivably have 10 girls and one boy, but this is balanced by the fact that half the families will have no girls at all.
The table below is drawn up using the simple rule that of the families who have a new girl one year all will try for a new baby, with half of them having a boy and half having a girl.
End of Year 1 Year 2 Year 3 Year 4 Year 5 Year Infinity
Total Boys 50,000 75,000 87,500 93,750 96,875 100,000
Total Girls 50,000 75,000 87,500 93,750 96,875 100,000
New Boys 50,000 25,000 12,500 6,250 3,125 0
New Girls 50,000 25,000 12,500 6,250 3,125 0
Let p(t) be the percentage of children that are male at the end of year t. How is this percentage expected to evolve through time?
I worked this little riddle out for myself also so it's probably fairly easy...
Right unusually let me tell you the answer first:-
p(t) ≠ f(t) p(t) = 50%
That is to say the percentage of children that are male is not a function of time and is always 50%. This may seem a little counter intuitive as we know that at some point in time a family could conceivably have 10 girls and one boy, but this is balanced by the fact that half the families will have no girls at all.
The table below is drawn up using the simple rule that of the families who have a new girl one year all will try for a new baby, with half of them having a boy and half having a girl.
End of Year 1 Year 2 Year 3 Year 4 Year 5 Year Infinity
Total Boys 50,000 75,000 87,500 93,750 96,875 100,000
Total Girls 50,000 75,000 87,500 93,750 96,875 100,000
New Boys 50,000 25,000 12,500 6,250 3,125 0
New Girls 50,000 25,000 12,500 6,250 3,125 0
Ant Sitting on Cubic Room
You are a bug sitting in one corner of a cubic room. You wish to walk (no flying) to the extreme opposite corner (the one farthest from you). Describe the shortest path that you can walk.
[bug in a room diagram]
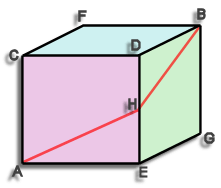
The problem phrased differently is that we have to get from point A to point B only moving along the walls.
The shortest route is shown it is A-H-B where H is the mid point of D-E.
The length of this route can easily be calculated, assume the cube has sides of length 1 unit (it doesn't matter what these units are, meters, feet, what ever) The distance A-H is the hypotenuse of a triangle 1 x ½ a quick bit of pythag tells us that A-H equals sqrt(5/4). Similarly H-B has the same length hence the total length is 2 x sqrt(5/4) this is actually equal to the square root of 5
A-H-B = sqrt(5) = 2.236
Some people think the shortest root is A-C-B or A-E-B or A-F-B etc. (they are all the same) this has a length of 1 + sqrt(2) ie. about 2.414.
Source : http://puzzles.nigelcoldwell.co.uk/three.htm
[bug in a room diagram]

The problem phrased differently is that we have to get from point A to point B only moving along the walls.
The shortest route is shown it is A-H-B where H is the mid point of D-E.
The length of this route can easily be calculated, assume the cube has sides of length 1 unit (it doesn't matter what these units are, meters, feet, what ever) The distance A-H is the hypotenuse of a triangle 1 x ½ a quick bit of pythag tells us that A-H equals sqrt(5/4). Similarly H-B has the same length hence the total length is 2 x sqrt(5/4) this is actually equal to the square root of 5
A-H-B = sqrt(5) = 2.236
Some people think the shortest root is A-C-B or A-E-B or A-F-B etc. (they are all the same) this has a length of 1 + sqrt(2) ie. about 2.414.
Source : http://puzzles.nigelcoldwell.co.uk/three.htm
One More Coins Puzzzle
You are given a set of scales and 90 coins. The scales are of the same type as above. You must pay $100 every time you use the scales.
The 90 coins appear to be identical. In fact, 89 of them are identical, and one is of a different weight. Your task is to identify the unusual coin and to discard it while minimizing the maximum possible cost of weighing (another task might be to minimizing the expected cost of weighing). What is your algorithm to complete this task? What is the most it can cost to identify the unusual coin?
The 90 coins appear to be identical. In fact, 89 of them are identical, and one is of a different weight. Your task is to identify the unusual coin and to discard it while minimizing the maximum possible cost of weighing (another task might be to minimizing the expected cost of weighing). What is your algorithm to complete this task? What is the most it can cost to identify the unusual coin?
Weigthing Coins one of Hardest Puzzle
You are given a set of scales and 12 marbles. The scales are of the old balance variety. That is, a small dish hangs from each end of a rod that is balanced in the middle. The device enables you to conclude either that the contents of the dishes weigh the same or that the dish that falls lower has heavier contents than the other.
The 12 marbles appear to be identical. In fact, 11 of them are identical, and one is of a different weight. Your task is to identify the unusual marble and discard it. You are allowed to use the scales three times if you wish, but no more.
Note that the unusual marble may be heavier or lighter than the others. You are asked to both identify it and determine whether it is heavy or light.
Most people seem to think that the thing to do is weigh six coins against six coins, but if you think about it, this would yield you no information concerning the whereabouts of the only different coin or the nature of it's difference as we already know that one side will be heavier than the other. It's worth mentioning that if this is used as an interview question this observation, by itself, is likely to get you a good portion of the way there.
So that the following plan can be followed, let us number the coins from 1 to 12. For the first weighing let us put on the left pan coins 1,2,3,4 and on the right pan coins 5,6,7,8.
There are two possibilities. Either they balance, or they don't. If they balance, then the different coin is in the group 9,10,11,12. So for our second one possibility is to weigh 9,10,11 against 1,2,3
(1) They balance, in which case you know 12 is the different coin, and you just weigh it against any other to determine whether it is heavy or light.
(2) 9,10,11 is heavy. In this case, you know that the different coin is 9, 10, or 11, and that that coin is heavy. Simply weigh 9 against 10; if they balance, 11 is the heavy coin. If not, the heavier one is the heavy coin.
(3) 9,10,11 is light. Proceed as in the step above, but the coin you're looking for is the light one.
That was the easy part.
What if the first weighing 1,2,3,4 vs 5,6,7,8 does not balance? Then any one of these coins could be the different coin. Now, in order to proceed, we must keep track of which side is heavy for each of the following weighings.
Suppose that 5,6,7,8 is the heavy side. We now weigh 1,5,6 against 2,7,8. If they balance, then the different coin is either 3 or 4. Weigh 4 against 9, a known good coin. If they balance then the different coin is 3, otherwise it is 4. The direction of the tilts can tell us whwther the offending coin is heavier or lighter.
Now, if 1,5,6 vs 2,7,8 does not balance, and 2,7,8 is the heavy side, then either 7 or 8 is a different, heavy coin, or 1 is a different, light coin.
For the third weighing, weigh 7 against 8. Whichever side is heavy is the different coin. If they balance, then 1 is the different coin. Should the weighing of 1,5, 6 vs 2,7,8 show 1,5,6 to be the heavy side, then either 5 or 6 is a different heavy coin or 2 is a light different coin. Weigh 5 against 6. The heavier one is the different coin. If they balance, then 2 is a different light coin.
Source : http://puzzles.nigelcoldwell.co.uk/one.htm
The 12 marbles appear to be identical. In fact, 11 of them are identical, and one is of a different weight. Your task is to identify the unusual marble and discard it. You are allowed to use the scales three times if you wish, but no more.
Note that the unusual marble may be heavier or lighter than the others. You are asked to both identify it and determine whether it is heavy or light.
Most people seem to think that the thing to do is weigh six coins against six coins, but if you think about it, this would yield you no information concerning the whereabouts of the only different coin or the nature of it's difference as we already know that one side will be heavier than the other. It's worth mentioning that if this is used as an interview question this observation, by itself, is likely to get you a good portion of the way there.
So that the following plan can be followed, let us number the coins from 1 to 12. For the first weighing let us put on the left pan coins 1,2,3,4 and on the right pan coins 5,6,7,8.
There are two possibilities. Either they balance, or they don't. If they balance, then the different coin is in the group 9,10,11,12. So for our second one possibility is to weigh 9,10,11 against 1,2,3
(1) They balance, in which case you know 12 is the different coin, and you just weigh it against any other to determine whether it is heavy or light.
(2) 9,10,11 is heavy. In this case, you know that the different coin is 9, 10, or 11, and that that coin is heavy. Simply weigh 9 against 10; if they balance, 11 is the heavy coin. If not, the heavier one is the heavy coin.
(3) 9,10,11 is light. Proceed as in the step above, but the coin you're looking for is the light one.
That was the easy part.
What if the first weighing 1,2,3,4 vs 5,6,7,8 does not balance? Then any one of these coins could be the different coin. Now, in order to proceed, we must keep track of which side is heavy for each of the following weighings.
Suppose that 5,6,7,8 is the heavy side. We now weigh 1,5,6 against 2,7,8. If they balance, then the different coin is either 3 or 4. Weigh 4 against 9, a known good coin. If they balance then the different coin is 3, otherwise it is 4. The direction of the tilts can tell us whwther the offending coin is heavier or lighter.
Now, if 1,5,6 vs 2,7,8 does not balance, and 2,7,8 is the heavy side, then either 7 or 8 is a different, heavy coin, or 1 is a different, light coin.
For the third weighing, weigh 7 against 8. Whichever side is heavy is the different coin. If they balance, then 1 is the different coin. Should the weighing of 1,5, 6 vs 2,7,8 show 1,5,6 to be the heavy side, then either 5 or 6 is a different heavy coin or 2 is a light different coin. Weigh 5 against 6. The heavier one is the different coin. If they balance, then 2 is a different light coin.
Source : http://puzzles.nigelcoldwell.co.uk/one.htm
Subscribe to:
Comments (Atom)