There are 100 light bulbs lined up in a row in a long room. Each bulb has its own switch and is currently switched off. The room has an entry door and an exit door. There are 100 people lined up outside the entry door. Each bulb is numbered consecutively from 1 to 100. So is each person.
Person No. 1 enters the room, switches on every bulb, and exits. Person No. 2 enters and flips the switch on every second bulb (turning off bulbs 2, 4, 6, …). Person No. 3 enters and flips the switch on every third bulb (changing the state on bulbs 3, 6, 9, …). This continues until all 100 people have passed through the room.
What is the final state of bulb No. 64? And how many of the light bulbs are illuminated after the 100th person has passed through the room?
Right first the answers: Light Bulb 64 is on. The total number of bulbs which are on including #64 is 10.
The working:-
There is a more eloquent way of working this but first lets look at a more brute force technique i used an Excel spread sheet:-
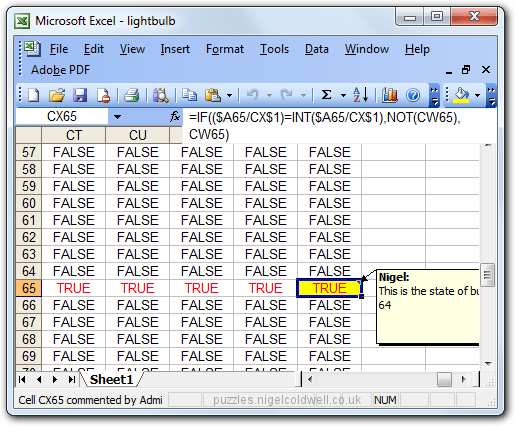
excel light switch puzzle
I'll just briefly explain to you the function used:
=IF(($A65/CX$1)=INT($A65/CX$1),NOT(CW65),CW65)
The 'if' command checks to see if the bulb number divided the person number is an integer that is to say it does the calculation twice (bulb number / person number) and rounds off one of the calculations to the nearest integer. It then compares the unrounded number to the rounded one. If these are the same then the person is entitled to switch that light bulb. Eg: Person 5 is entitled to switch bulb 50 but not 51, do the sum if you like.
I have included the Spread sheet, you will need Winzip and Excel to view the file:
lightbulb.zip - 46.9KB
A More eloquent approach.
First think who will operate each bulb, obviously person #2 will do all the even numbers, and say person #10 will operate all the bulbs that end in a zero. So who would operate for example bulb 48:
Persons numbered: 1 & 48, 2 & 24, 3 & 16, 4 & 12, 6 & 8 ........
That is all the factors (numbers by which 48 is divisible) will be in pairs. This means that for every person who switches a bulb on there will be someone to switch it off. This willl result in the bulb being back at it's original state.
So why aren't all the bulbs off?
Think of bulb 36:-
The factors are: 1 & 36, 2 & 13, 6 & 6
Well in this case whilst all the factors are in pairs the number 6 is paired with it's self. Clearly the sixth person will only flick the bulb once and so the pairs don't cancel. This is true of all the square numbers.
There are 10 square numbers between 1 and 100 (1, 4, 9, 16, 25, 36, 49, 64, 81 & 100) hence 10 bulbs remain on.
source : http://puzzles.nigelcoldwell.co.uk/six.htm
Person No. 1 enters the room, switches on every bulb, and exits. Person No. 2 enters and flips the switch on every second bulb (turning off bulbs 2, 4, 6, …). Person No. 3 enters and flips the switch on every third bulb (changing the state on bulbs 3, 6, 9, …). This continues until all 100 people have passed through the room.
What is the final state of bulb No. 64? And how many of the light bulbs are illuminated after the 100th person has passed through the room?
Right first the answers: Light Bulb 64 is on. The total number of bulbs which are on including #64 is 10.
The working:-
There is a more eloquent way of working this but first lets look at a more brute force technique i used an Excel spread sheet:-

excel light switch puzzle
I'll just briefly explain to you the function used:
=IF(($A65/CX$1)=INT($A65/CX$1),NOT(CW65),CW65)
The 'if' command checks to see if the bulb number divided the person number is an integer that is to say it does the calculation twice (bulb number / person number) and rounds off one of the calculations to the nearest integer. It then compares the unrounded number to the rounded one. If these are the same then the person is entitled to switch that light bulb. Eg: Person 5 is entitled to switch bulb 50 but not 51, do the sum if you like.
I have included the Spread sheet, you will need Winzip and Excel to view the file:
lightbulb.zip - 46.9KB
A More eloquent approach.
First think who will operate each bulb, obviously person #2 will do all the even numbers, and say person #10 will operate all the bulbs that end in a zero. So who would operate for example bulb 48:
Persons numbered: 1 & 48, 2 & 24, 3 & 16, 4 & 12, 6 & 8 ........
That is all the factors (numbers by which 48 is divisible) will be in pairs. This means that for every person who switches a bulb on there will be someone to switch it off. This willl result in the bulb being back at it's original state.
So why aren't all the bulbs off?
Think of bulb 36:-
The factors are: 1 & 36, 2 & 13, 6 & 6
Well in this case whilst all the factors are in pairs the number 6 is paired with it's self. Clearly the sixth person will only flick the bulb once and so the pairs don't cancel. This is true of all the square numbers.
There are 10 square numbers between 1 and 100 (1, 4, 9, 16, 25, 36, 49, 64, 81 & 100) hence 10 bulbs remain on.
source : http://puzzles.nigelcoldwell.co.uk/six.htm
No comments:
Post a Comment