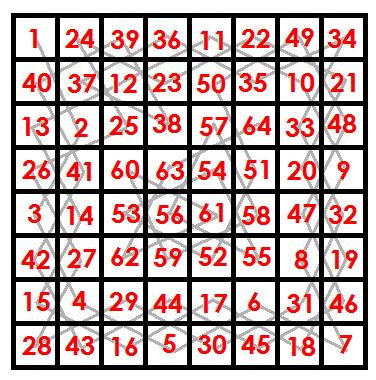
Set 1-8 in these 8 boxese such that consecutive numbers wont intersect vertically/horizontally or diagonally

                                                                   
                                             
    -----
    |    |
    |    |
 -------------
 |  |    |    |
 |  |    |    |
 --------------
 |  |    |    |
 |  |    |    |
 --------------
    |    | 
    |    | 
    ------

How many regions (open or closed) can n straight lines give at the maximum?

Let f(n) denote the number of regions for n lines no three of which coincide in one point. This latter condition will guarantee the maximum. Obviously, f(0)=1, f(1)=2, f(2)=4, f(3)=7, etc.

Now, given n-1 lines, there are already f(n-1) regions. With the introduction of the n-th line, imagine the points of intersection of the pre-existing n-1 lines fall on one side of the n-th line. So, on one side of the n-th line -- where the points of intersection lie -- you still have f(n-1) regions, whereas on the other side of the n-th line, you now have n regions. So, for these n lines before us, the total number f(n) of regions must be equal to f(n-1)+n.

So, f(n)=f(n-1)+n. With the initial condition(s) given earlier, this gives us f(n)=1+n(n+1)/2.

Josephus Problem - Puzzle

A Triangle Puzzle

three points are randomly chosen on a circle.what the probability that
1.triangle formed is right angled triangle.
2.triangle formed is acute angled triangle.
3.triangle formed is obtuse angled triangle.

Let the three vertices be A, B, C. We denote the angle at
center by the arcs AB, BC, CA by x, y, z.

x + y + z = 360.

Hence, the sample space can be represented by the region
surrounded by lines

x > 0,
y > 0 , and
x + y < 360. For the acute angled triangle ABC max(x, y, z) < 180, i.e., x < 180, y < 180, and x + y > 180

It can be easily seen that the three constraints form a
region which has exactly 1/4-th area of the original
sample space.

Solution Given abc

Tumblers on a Rotating Table- 3 Glass & 4 Glass

The three cups problem is a mathematical puzzle. Starting with three cups place one upside down and two right side up. The objective is to eventually turn all cups right side up in six moves. You must turn exactly two cups over each turn.
[edit] Solution

The puzzle is impossible. An even number of cups are facing up and you are allowed to turn two over at a time. Since an even plus an even is an even, not an odd, no number of even flips will ever get all the three cups face up. You need an odd number of cups facing up, so the problem is impossible. The possible version of this puzzle is to start with two cups facing down and one cup facing upward. This is possible. Turn up an even number (two) of cups, and all the cups are facing up; an odd plus an even is an odd (1+2 = 3).






Tumblers on a Rotating Table Puzzle :

A blind gnome and an evil goblin take turns to play a game. Four tumblers are placed at the corners of a square table. The initial configuration of the tumblers (facing up or facing down) is chosen by the evil goblin. When the blind gnome gets his turn, he is allowed to specify a subset of the four tumblers and flip them simultaneously. To be precise, he may choose “one tumbler”, “two diagonally opposites”, “two adjacent”, “three tumblers” or “four tumblers” lying in front of him, and flip them simultaneously. After flipping, if all four tumblers are upright, he wins the game! Otherwise, the game continues and the evil goblin is allowed to rotate the table by an amount of his choice. Can the blind gnome win the game with a deterministic strategy?

Solution :


If there were only two cards, then “flip both” — “flip one” — “flip both” would ensure a victory for the blind gnome. For the case of four cards, let F denote “all four cards”, A denote “two adjacent cards”, D denote “two diagonally opposite cards”, O denote “one card”. Then the following 15-step sequence ensures victory for the blind gnome: F, D, F, A, F, D, F, O, F, D, F, A, F, D, F. The procedure can be generalized to 2^n cards. This problem is studied in detail by Ehrenborg and Skinner (see bibliography below); they call it “The Blind Bartender’s Problem”.
A variant of the above problem allows the blind gnome to first “touch” any t out of n tumblers on a polygonal table with n sides. Touching allows the gnome to deduce which of the t tumblers he touched are upright, and then to decide which of these t tumblers to flip. It was this variant that was originally published in Martin Gardner’s article in Feb 1979. For four tumblers, the blind gnome can win in five moves, as Gardner showed in his subsequent article in Mar 1979. The problem generated quite some interest. Two pairs of mathematicians independently proved that the blind gnome can win with a deterministic strategy if and only if t ≥ n(p-1)/p where p is the largest prime factor of n (Lewis and Willard in 1980; Laaser and Ramshaw 1981). These proofs are quite involved

Whats The Age of 3 Childs .?????

A man walks into a bar, orders a drink, and starts chatting with the bartender. After a while, he learns that the bartender has three children. "How old are your children?" he asks. "Well," replies the bartender, "the product of their ages is 72." The man thinks for a moment and then says, "that's not enough information." "All right," continues the bartender, "if you go outside and look at the building number posted over the door to the bar, you'll see the sum of the ages." The man steps outside, and after a few moments he reenters and declares, "Still not enough!" The bartender smiles and says, "My youngest just loves strawberry ice cream." How old are the children?




Answer :

First, determine all the ways that three ages can multiply together to get 72:


72 1 1 (quite a feat for the bartender)
36 2 1
24 3 1
18 4 1
18 2 2
12 6 1
12 3 2
9 4 2
9 8 1
8 3 3
6 6 2
6 4 3
As the man says, that's not enough information; there are many possibilities. So the bartender tells him where to find the sum of the ages--the man now knows the sum even though we don't. Yet he still insists that there isn't enough info. This must mean that there are two permutations with the same sum; otherwise the man could have easily deduced the ages.

The only pair of permutations with the same sum are 8 3 3 and 6 6 2, which both add up to 14 (the bar's address). Now the bartender mentions his "youngest"--telling us that there is one child who is younger than the other two. This is impossible with 8 3 3--there are two 3 year olds. Therefore the ages of the children are 6, 6, and 2.

Question

A variant of the problem is for the sum of the ages to be 13 and the product of the ages to be the number posted over the door. In this case, it is the oldest that loves ice cream. Then how old are they?


In the sum-13 variant, the possibilities are:
11 1 1
10 2 1
9 3 1
9 2 2
8 4 1
8 3 2
7 5 1
7 4 2
7 3 3
6 6 1
6 5 2
6 4 3

The two that remain are 9 2 2 and 6 6 1 (both products equal 36). The final bit of info (oldest child) indicates that there is only one child with the highest age. This cancels out the 6 6 1 combination, leaving the childern with ages of 9, 2, and 2.

Chess Queen Puzzle

Imagine there are infinite number of Queens (Chess Game Piece) with u. Find the minimum number of queens required so that every square grid on the chess board is under the attack of a queen. Arrange this minimum no. of Queens on a chess board.



to solve it we have to think all possible combination. because we have to find out the one can easily solve it if he has strong foundation of backtracking algorithm its the geeks way to solve . although it can also be solve by trying all possible combinatios thats the normal way

start by putting queen at all position where i=j e.g. 1,1, 2,2 3,3, & so on
so then we have 8 queens like It can also be keeping one at diagonal (0,0) (1,1) (2,2) (3,3) (4,4) (5,5) (6,6) (7,7)

can we do better ..??

as we know This problem has more than one solutions. I found one with 6 queens placed at (0,0), (1,7), (2,1), (3,4), (4,2), (6, 3) now if we rotate the chess board then we can get other solution so in this case we need 6 queen can we do still do better..?? think again



it requires much deep thinking then i was able to come up with two more solution that requires 5 queens & i think that are minimum number of queens we are looking for ...

1st (1,1) (3,4) (3,6) (4,2) (5,5)
2nd (0,0) (1,7) (2,4) (4,0), (7,6)

Queen Needed 5

Feel Free to Update & Optimize Th Solution

Find 3 Fastest Horses from set of 25 Horses

There are 25 horses and only five tracks in a race (i.e., you can race 5 horses at a time). There is no stop clock !! Assume that there are no ties.

1: What is the minimum number of races needed to determine the 3 fastest horses in order from fastest to slowest ?

We group the 25 horses in 5 groups each containing 5 horses.In each of first five races we will rank each five horsesA, B,C,D and E ( A : fastest and E: slowest) in the group.

1A 1B 1C 1D 1E
2A 2B 2C 2D 2E
3A 3B 3C 3D 3E
4A 4B 4C 4D 4E
5A 5B 5C 5D 5E


In the sixth race ( among the first of each group) we will get the fastest horse and rank these five horses 1A,2A,3A,4A & 5A (1A : fastest and 5A slowest)
Similarly .just select the fastest of the remaining horses from each row for the race.

Now we have got the fastest horse 1A and will also set nomenclature for each horses.
The fastest of the remaining horses in the row will take part.For e.g. the seventh race will be between 1B & 2A (no need to run 3A,4A & 5A)for determining
2nd fastest horse.

The 8th race will determine the third place and it will be between 1C and 2B ( in case 1B wins 7th race) or among 1B,2B & 3A ( in case 2A wins 7th race).

The 9th race will determine the 4th place and the 10th race will determine 5th place.

And moving on 25 th race will determine 20th place.The 26th race will tel the remaining 5 ranks.



Follow Up minimum number of races needed to find
1:....... to rank all of them from fastest to slowest ?
2:....... to find the top k fastest horses ?


* min number of races to rank all of them

sol:-

1. I can re-phrase this question to ask the min number of races to get 25 fastest horses.
2. You need 6 races to get the fastest ranked (steps 1 thru 3).
3. After that every race will give you the next fastest.
4. We can continue this till we have got the 20 fastest horses. After that we just need 1 race to rank the remaining 5.

total = 6 (to get rank 1) + 19 (to get rank 2-20) + 1 (to get rank 21-25) = 26

* min number of races to get k fastest horse

sol:-

5 + k (for k <= 20 )
26 (otherwise)

How many regions (open or closed) can n straight lines give at the maximum?

Let f(n) denote the number of regions for n lines no three of which coincide in one point. This latter condition will guarantee the maximum. Obviously, f(0)=1, f(1)=2, f(2)=4, f(3)=7, etc.

Now, given n-1 lines, there are already f(n-1) regions. With the introduction of the n-th line, imagine the points of intersection of the pre-existing n-1 lines fall on one side of the n-th line. So, on one side of the n-th line -- where the points of intersection lie -- you still have f(n-1) regions, whereas on the other side of the n-th line, you now have n regions. So, for these n lines before us, the total number f(n) of regions must be equal to f(n-1)+n.

So, f(n)=f(n-1)+n. With the initial condition(s) given earlier, this gives us f(n)=1+n(n+1)/2.

we can use induction to prove the same,

Base case:
if n = 1, regions (planes) = 2

Induction Hypothesis:
Addition of a new line adds
---------------------------------------------
|n
---------------------------------------------

regions to the regions formed by previous
---------------------------------------------
|n-1
---------------------------------------------
lines, i.e.

f(n) = n + f(n-1)

Upon simplifying the above, we get f(n) = 1 + n(n+1)/2

Knight Tour - Yet Another Chess Problem

Source : Heard From My Friend Who Went to Crack Amazon

The Knight's Tour is a famous chess problem, in which a knight starts on the top-left square of an ordinary chessboard and then makes 63 moves, landing on every square of the chessboard exactly once (except for the starting square).

Can you complete the Knight's Tour? For a further challenge, can you find a "closed" solution, meaning that the knight can make a 64th move to land back on the starting square (thus making the solution circular)?





Solution
This pictures shows a non-cyclical solution. The strategy is to essentially cover the border (outer 3 rows/columns) first, and then cover the inner part of the board. We'll leave a cyclical solution as a challenge to the reader




More Info
http://en.wikipedia.org/wiki/Knight%27s_tour

9 Digit Number Problem Every nth number formed by n digit is Divided By Every nth digit

Arrange the digits 0 to 9 such, that the number formed by the
first digit is divisible by 1, the number formed by the first two
digits is divisible by 2, that formed by the first three digits
divisible by 3, and so forth, thus the number formed by the first
9 digits will be divisible by 9 and that formed by all 10 digits
divisible by 10.

Here is what we would do.

_ _ _ _ _ _ _ _ _ _

those are my ten blanks.

Now let's start asking questions.

Since the whole thing has to be divisible by 10, the last number
must be a zero.

And since the first five digits must be divisible by 5, the fifth
digit must be a 5 or 0, but we have already used 0 so it must be a
five.

One last quickie is that the 2nd, 4th, 6th, and 8th and last
digits must be even, so all the rest are odd

So let's look at we have. I'll write the digits that could go in a
certain place under where they could go:


_ _ _ _ 5 _ _ _ _ 0
1 2 1 2 2 1 2 1
3 4 3 4 4 3 4 3
7 6 7 6 6 7 6 7
9 8 9 8 8 9 8 9

Now things get trickier.

Let's start with the 4th spot.

Any number is divisible by 4 if the last two digits are divisible
by 4

So what are the two-digit numbers divisible by 4 that begin with
an odd number that is not 5?

12 16 32 36 72 76 92 96

Hey, so the 4th digit is either a 2 or a 6.

Now, let's look at the 8th digit. If the first 8 digits are
divisible by 8, then they are divisible by 4 also. So if we apply
the same logic as above, we find that the 8th digit is either a 2 or
a 6.

So spaces 2 and 6 must be 4 or 8.

That narrows it down. So we have this:

_ _ _ _ 5 _ _ _ _ 0
1 4 1 2 4 1 2 1
3 8 3 6 8 3 6 3
7 7 7 7
9 9 9 9



Now for my next trick let's recall that every third space must be
divisible by 3. So every three numbers must sum to be divisible
by 3.

In particular spaces 4, 5, and 6 must sum to 3, and we already
have a five. So either we have

2 5 8 or 6 5 4

in positions 4, 5, and 6.

That is good stuff. That means we have either this:

_ 4 _ 2 5 8 _ 6 _ 0
1 1 1 1
3 3 3 3
7 7 7 7
9 9 9 9

or this:

_ 8 _ 6 5 4 _ 2 _ 0
1 1 1 1
3 3 3 3
7 7 7 7
9 9 9 9

Let's check each of the four digits we could put in the 8th place.
Since a number is divisible by 8 if its last 3 digits are, we need
number in the 6th, 7th, and 8th places to be divisible by 8. We see
that 816 and 896 work in the first case, and 432 and 472 work in the
second case. So we have:

_ 4 _ 2 5 8 _ 6 _ 0
1 1 1 1
3 3 9 3
7 7 7
9 9 9

or this:

_ 8 _ 6 5 4 _ 2 _ 0
1 1 3 1
3 3 7 3
7 7 7
9 9 9


Let's look at the 9th place now. Recall that 1+2+3+4+5+6+7+8+9 = 45,
so we don't need to worry about the 9th place - it will always work
out.

Let's look at the 1st and 3rd places. In case 1, only 147 and 741 are
options. In case 2, we could have 183, 189, 381, 387, 783, 789, 981, or
987. Note that 387 and 783 don't work, because then we don't have any
digits left for the 7th digit.

So our first case becomes:

_ 4 _ 2 5 8 9 6 3 0
1 1
7 7

We can just check the two numbers this can give rise to, namely 1472589630
and 7412589630. Since neither of them are divisible by 7, case one must be
a dead end. So we have to work with case two if we want a solution:

_ 8 _ 6 5 4 _ 2 _ 0
1 1 3 1
3 3 7 3
7 7 7
9 9 9

(and the first 3 digits are 183, 189, 381, 789, 981, or 987)

If we look at the 7th, 8th, and 9th digits to see if we can get them to sum
to three, we see that only 321, 327, 723, and 729 are options.

So which of our options for digits 1,2,3 and 7,8,9 can we use together? In
order to not repeat digits, we could use these:

183 and 729
189 and 327
189 and 723
381 and 729
789 and 321
981 and 327
981 and 723
987 and 321

This means that the only possible solutions to the puzzle are these:

1836547290
1896543270
1896547230
3816547290
7896543210
9816543270
9816547230
9876543210

This is now a small enough number of cases that we can check them by hand.
The first thing we should do is check the first 7 digits for divisibility by
seven. Here are the results:

1836547/7 = 262363.857142857...
1896543/7 = 270934.714285714...
1896547/7 = 270935.285714286...
3816547/7 = 545221
7896543/7 = 1128077.57142857...
9816543/7 = 1402363.28571429...
9816547/7 = 1402363.85714286...
9876543/7 = 1410934.71428571...

There are n buses in a city. Each of them carries at most m passengers. Find the probability that at least two of them carry the same number of passen

There are n buses in a city. Each of them carries at most m passengers. Find the probability that at least two of them carry the same number of passengers.



This is equal to 1-(probability that they all carry different number of passengers). That probability in paranthesis is equal to (m+1)!/((m+1-n)! * (m+1)^n). This is given that (m+1) >= n. If (m+1) < n, then the probability is 1.

- m+1 because maximum m passengers mean m+1 different possiblities (a bus could carry 0 passengers).
- The first bus has (m+1) possibilities in terms of number of passengers. The second has m+1, the third has m+1 and so on. Total number of orderings possible is (m+1) ^ n.
- For the number of passengers to be different in each bus, first bus has m+1 possibilities, second has m, third has m-1 nd so on. For n buses, this is equal to (m+1)!/(m+1-n)!. Dividing this by (m+1)/n gives the possibility. Subtract this number from one to find at least two buses with the same amount of passengers.


Solved by James

The Wire Identification Problem

There is a bunch of 120 electrical cables laid under the ground. The cables are 10 KM in length and both ends of each wire are out in open.




We need to identify and label the cables 1-120. All you have is a circuit completion detector bulb.(i.e. if you join same side ends of any two cables and then on the other side apply the bulb to corresponding 2 ends then bulb will light up, but to detect this way you have to make a 10 KM trip)

How would you identify each cable in minimum number of trips.

Solution

We need to identify and label the cables 1-120. As you might have guessed, the only way to gain information in this setup is to connect some set of wires at one end, walk up to the other end, and test for conductivity. The process may have to be repeated many times before a complete labeling can be constructed. And since each such step involves walking across 10 KM, we wish to solve the problem with the least number of trips.

How would you identify each cable in minimum number of trips?

Answer:
Boundary Condition: If we have just 2 wires, there’s really nothing we can use to break the symmetry of the situation.

Solution: At the first end, connect pairs of wires together, leaving two wires unconnected. Go to the other end. Find a pair of connected wires, andnumber them #2 and #3. Find another pair and label them #4 and #5. Repeat for all of the pairs, with the last pair labeled #118 and #119. There remain two wires that are not connected to each other. Label one of these #1 and the other #120.

Now at second end, connect #1 to #2, #3 to #4, etc, leaving #119 and 120 unconnected. Go back to the first end. One of the originally unconnected wires still is unconnected. Label it #120 and label the other originally connected wire #1. Now find the wire connected to #1 and label it #2. The wire that originally was connected with new wire #2 can be labeled #3. The wire that is now connected to the newly labeled #3 is #4. In this way, all of the wires can be identified on both ends in two trips (one round trip). If it is necessary to disconnect the connections at the other end, a third trip is necessary.

Below is an execution diagram for 6 wires. We have to label wires from 1-6.





Source

http://ashutoshmehra.net/blog/2009/09/wire-identification-problem/

6 Riddles

QUESTIONS:

1) The Elder Twin
One day Kerry celebrated her birthday. Two days later her older twin brother, Terry, celebrated his birthday.
How could this happen?

2) Manhole Covers
Why is it better to have round manhole covers than square ones?

This is logical rather than lateral, but it is a good puzzle which can be solved by lateral thinking techniques. It is supposedly used by a very well-known software company as an interview question for prospective employees.

3) The Deadly Party
A man went to a party and drank some of the punch. He then left early. Everyone else at the party who drank the punch subsequently died of poisoning.
Why wasn't the first guy poisoned?

4) Heaven
A man died and went to Heaven. There were thousands of other people there. They were all naked and all looked as they died at the age of 21. He looked around to see if there was anyone he recognized. He saw a couple and he knew immediately that they were Adam and Eve.
How did he know?

5) Trouble with Sons
A woman had two sons who were born on the same hour of the same day of the same year. But they were not twins.
How could this be so?

6) The Man in the Bar
A man walks into a bar and asks the barman for a glass of water. The barman pulls out a gun and points it at the man. The man says `Thank you' and walks out.
Why?

This puzzle has claims to be the best of the genre. It is simple in its statement, absolutely baffling and yet with a completely satisfying solution. Most people struggle very hard to solve this one yet they like the answer when they hear it or have the satisfaction of figuring it out.





ANSWERS:

1) At the time she went into labor, the mother of the twins was traveling by boat. The older twin, Terry, was born first early on March 1st. The boat then crossed the International Date line (or anytime zone line) and Kerry, the younger twin, was born on February the 28th. In a leap year the younger twin celebrates her birthday two days before her older brother.

2) A square manhole cover can be turned and dropped down the diagonal of the manhole. A round manhole cannot be dropped down the manhole. So for safety and practicality, all manhole covers should be round.

3) The poison in the punch came from the ice cubes. When the man drank the punch the ice was fully frozen. Gradually it melted, poisoning the punch.

4) He recognized Adam and Eve as the only people without navels. Because they were not born of women, they had never had umbilical cords and therefore they never had navels.

This one seems perfectly logical but it can sometimes spark fierce theological arguments!

5) They were two of a set of triplets (or quadruplets etc.)

This simple little puzzle stumps many people. They try outlandish solutions involving test-tube babies or surrogate mothers. Why does the brain search for complex solutions when there is a much simpler one available?

6) The man had hiccups. The barman recognized this from his speech and drew the gun in order to give him a shock. It worked and cured the hiccups - so the man no longer needed the water.

The is a but a difficult one to solve. It is a perfect example of a seemingly irrational and incongruous situation having a simple and complete explanation. Amazingly this classic puzzle seems to work in different cultures and languages.

King Bear & Poison ..Very Common & Tough Puzzle

Problem : A king has a wine cellar with 100 drums of wine. A traitor sneaked into his wine cellar to poison the drums. He could mix poison in only one of the drums when guards caught him. However, guards could not see which one drum was poisoned. Our king being a drunkard wishes to be able to drink wine as soon as possible but safely. The poison guarantees that the person drinking the wine would die in 10 days.

Being a king, he can order his servants to drink wine from the drums to find out poisonous drum. However, he wishes does not want to risk lives of too many servants.

1) King wishes to be able to drink some wine on 11th day. How many servant would be needed to take the risk of drinking wine before figuring out a harmless wine drum?

2) King wishes to throw a grand party on 11th day. How many servant would be needed for figuring out the poisonous wine drum?

Solution :

The solution to the first problem is extremely simple and obvious. Only one servant need to drink any one of the wine drum. If the servant dies, all the other drums are harmless. If he does not die, we can guarantee that at least that one wine-drum is harmless.

Well, second problem has actually two sides to it. Say for example, king wishes that number of servant to be put on stake can be arbitrarily large, but the number of servant died during the process should be less. Then, we need 99 servant for each wine drum. At most one servant would die in this case.

However, what if we want to minimize the number of servants to be put on stake? Initially I went on a very wrong direction. That was to use prime factorization of every number from 1 to 100. For example, there will be a servant drinking from wine-drums which are numbered in multiple of 2, and similarly another servant for multiple of 5. So, we would be able to detect number 10 as the poisonous drum if both of them dies. Using this multiple scheme, number of servant needed would be

2,4,8,16,32,64

3,9,27,81

5,25

7,49

all primes number between 1 to 100 which has not appeared in the above list.
Basically, the number comes out to be huge. Certainly a very very bad solution.

A good solution would be to arrange wine-drums in 10×10 maze. We would need only 20 servant. 10 servant for the row and 10 for the column. So when in 10 days i-th servant for row and j-th servant for column dies, we would know that the drum located at (i,j) is the culprit. But still we are far from the best solution.

We can visualize the maze in three dimension. 5x5x5 would need only 15 servants. Of course, there would be some spots empty in the maze, but that does not matter.6x6x3 = 15. Going ahead we can have 5x5x4=14.

It seems we can still push it further. We can visualize the maze in four dimension. 4x3x3x3 = 13. This is the least possible number I could find. I don’t know whether we can push it still further down. If you can figure out a still smaller number, please comment on this post.


Soln By –Saurabh Joshi from his blog me.maths & puzzle
i found its interesting so i pasted here

Another Hat Color Problem

The Island - One puzzle a day - Puzzle Buddies
100 men were captured and prisoned in an island.the island is guarded by a genie.
Everyday genie takes prisoners out.genie places them in a circle so that everyone can see each other,then all the prisoners are blindfolded. Genie then places hats on prisoners head,some of them are white and some of them are red.their folds will be opened after the genie places hats.

On genie's command the prisoners with white hat should step forward.They will be set free if only the men with white hat steps forward.
If any one without white hat steps forward,genie executes all of them
If no one steps forward,the same game will be repeated the next day,if the game is repeated,each prisoner will get the same hat that they got on the first day

Prisoners are not allowed to communicate with each prisoner.if communicated all of them will be executed.prisoners are not allowed to see the hat that they are wearing
At least one white hat is given, and all prisoners are aware of this.

how many days did it take for the prisoners to get out if genie gave "n" white hats where 1<=n<=100, and how did they do it?



Solution:
Let us say there is one white hat,the answer is simple.the prisoner wearing white hat sees no other white hat and he steps forward.
Now let us take two white hats.No body comes forward on the first day,because the prisoners wearing white hat sees one white hat.On the second day since no body has come forward they both know there must be two white hats and one he can see and other must be his own.so they come forward on second day.
Similarly if there are three white hats they will not come out on second day.it will take three days.
and so on..for "n" it will take n days

Monty Hall Problem

You are a contestant on a game show. You have three closed doors in front of you. One of the doors has a car behind it and the other two doors have nothing. You have to choose a door to open.

You have with you a Magic Watch.
- Whenever you ask the watch a question with a yes/no answer, it will blink either red or blue.
- One of the colors represents 'yes' and the other 'no'.
- You don't know which color means what. (gotcha!)
- You are allowed to ask the watch only 2 questions before you make your decision.

Which questions would you ask and how would you choose the door to open?

The puzzle might have a number of solutions and this is one of them.

Solution:

The contestant should ask the following two questions:
1) If I asked whether the car was behind door 1, would you blink red?
2) If I asked whether the car was behind door 2, would you blink red?

There are two cases here:
a) red = no, blue = yes:

The watch can answer in 4 different ways:
1) red, blue:
From the answer to the 1st question, car is behind door 1.
From the answer to the 2st question, car is not behind door 2.
2) blue, red:
From the answer to the 1st question, car is not behind door 1.
From the answer to the 2nd question, car is behind door 2.
3) blue, blue:
From the answer to the 1st question, car is not behind door 1.
From the answer to the 2nd question, car is not behind door 2.
4) red, red:
From the answer to the 1st question, car is behind door 1.
From the answer to the 2nd question, car is behind door 2.
b) red = yes, blue = no:

The watch can answer in 4 different ways:
1) red, blue:
From the answer to the 1st question, car is behind door 1.
From the answer to the 2st question, car is not behind door 2.
2) blue, red:
From the answer to the 1st question, car is not behind door 1.
From the answer to the 2nd question, car is behind door 2.
3) blue, blue:
From the answer to the 1st question, car is not behind door 1.
From the answer to the 2nd question, car is not behind door 2.
4) red, red:
From the answer to the 1st question, car is behind door 1.
From the answer to the 2nd question, car is behind door 2.

Observe that the conclusions are exactly the same for the same answer set irrespective of the color code.
Hence, when the watch answers:
1) red, blue: Pick door 1.
2) blue, red: Pick door 2.
3) blue, blue: Pick door 3.
4) red, red: This outcome is impossible since it implies that the car is behind door 1 as well as door 2.

How can you get a fair coin toss

Interview question: How can you get a fair coin toss if someone hands you a coin that is weighted to come up heads more often than tails?

The story of these types of questions starts at the software giant Microsoft who pioneered the use of puzzle type question, where the aim is to test the interviewers problem solving skills and creativity. It's ironic that these type of questions are no longer asked in Microsoft job interviews, but the rest of the software industry hasn't caught on.



The solution is to toss the coin twice, which gives four possible outcomes:
H (heads) followed by H, probability of this is pH * pH
H followed by T (tails), probability of this is pH * pT
T followed by H, probability of this is pT * pH
T followed by H, probability of this is pT * pT
Looking at the above outcomes we can see that HT (H followed by T) is just as likely as TH,
So to get a fain coin toss, toss the coins and use HT or TH as fair outcomes of the toss, and discard the results of TT and HH.

Weigh System With More Explaination..How Many Weight We Needs..???

Puzzle: You have a common balance with two sides. You can only keep weighs on one side. You have to weigh items from 1 to 1000 weight units with integral weights only.
What is the minimum number of weights required and what will be their weights?
Eg. With 2 weights one of 1 weight unit and other of 3 weight unit you can measure 1, 3 and 4 only.
Note: Don't forget to visit us again. Answer to the puzzle will be posted tomorrow. You can provide your answer in comments.

Solution: This puzzle is an easy puzzle as to make any odd number you need all other even numbers and one 1.
So only one odd number is needed to make all odd numbers. Now you are left with all even numbers. All even numbers are base 2 and thus can be though of as binary representation. To make 1000 you need at most 10 bits(1111101000). You can make any number below 1000 from these bits.
So the answer is 10 weights required. 1, 2, 4, 8,16, 32, 64, 128, 256, 512.

Puzzle: This is part 2 of puzzle posted Above. The puzzle is that you have to weigh 1 to 1000 using a common balance scale with minimum number of weighs. This time you can put wights on both sides.
You can check Part 1 of this puzzle How many weights? Puzzle Part 1.
Note: Don't forget to visit us again. Answer to the puzzle will be posted tomorrow with winner's name. You can provide your answer in comments.

Solution: The answer is series of base 3 i.e. 1, 3, 9, 27, 81, 243 and 729.
We can start from smallest number 1. To measure 1 we definitely need 1.
To measure 2 we need to look for highest number possible. We can measure 2 by using 3(3-1 = 2). So we need 1 and 3.
Now to measure 4 we can use 1 and 3 both (1+ 3). To measure 5 again we will look for highest possible number. 9 is highest possible number (9-4 = 5). We can measure up to 13 using these weights.

Continuing the same way we can deduce that a series of base 3 is required, thus 1, 3, 9, 27, 81, 243, 729.


Puzzle: This is the 3rd part of weighing puzzles. You can check Part 2 and Part 1.
You have to weigh 125 packets of sugar with first one weighing 1 lb, second 2 lb, third 3 lb and so on.You can only use one pan of the common balance for measurement for weighing sugar, the other pan has to be used for weights.
The weights have to put on to the balance and it takes time. Time taken to move weights is equal to the number of weights moved.
Eg. So if you are weighing 5 lb using 3lb and 2 lb weight then you have to lift both these weights one by one and thus it will take 2 unit time. If you have to measure only 3lbs it will take only 1 unit time. Now if we have to measure sugar packets of weights 1,3,4 using weights 1 and 3 only. For this first we measure 1 lb, with 1 unit of time, we place 3 lb along with 1 lb and measure 4kg with again 1 unit of time, and finally we move 1kg out of pan to measure 3kg in 1 unit of time. So in 3 units of time we could measure 1,3 and 4lb using weights 1 and 3 only.

Now you have to make sugar packets of all weights from 1 to 125 in minimum time, in other words in minimum movement of weights. The question here is to find out the minimum number of weighs needed and the weight of each the weights used and the strategy to be followed for the creation of 125 packets of sugar.
Note: Don't forget to visit us again. Answer to the puzzle will be posted tomorrow with winner's name. You can provide your answer in comments.
Source: Classic Puzzles
Solution: Amazing explanation provided by Kasturi.
You will need the weights 1, 2, 4, 8, 16, 32 and 64 i.e. 7 weights. You can measure 125 packets in 125 movements. The strategy to be followed is this:
Put 1: measure 1, weights in pan 1

To measure further you need to use a new weight.
Put 2: measure 3, weights in pan 1,2
Remove 1: measure 2, weights in pan 2

Thus, by adding the next smallest weight to the pan i.e. 2, we can measure all weights below 4 in total 3 movements.

To measure further you need to use a new weight.
Put 4: measure 6, weights in pan 2,4
Remove 2: measure 4, weights in pan 4
Put 1: measure 5, weights in pan 1,4
Put 2: measure 7, weights in pan 1,2,4

Thus, by adding the next smallest weight to the pan i.e. 4, we can measure all weights below 8 in total 7 movements.

Following the same strategy, whenever we have measured all weights below n, add n and we can measure measure all the weights below 2n in 2n-1 movements.
Eventually, we can measure 125 packets in 125 movements.

Pills Puzzle

A person was prescribed to take two pills (tablets), one each, from the two bottles viz. Bottle A and Bottle B, daily. The tablets are exactly look alike.

The medicines have to be taken exactly one tablet from each bottle, neither less nor more, else the medicines will not be effective.

One fine day, the patient popped out one tablet from Bottle A, but while taking the tablet from bottle B, by mistake, two tablets spilled over. Now he has three tablets in his hand, and he can't put back the extra tablet to Bottle B as all the tablets are identical in looks.

He has to ensure that he takes exactly one tablet from each of the bottle and at the same time he must avoid any wastage of the medicine.

Constraints:
1. Both bottles have equal number of tablets, say 30.
2. Tablets from both the bottles look exactly identical.
3. Medicine is very costly, so any kind of wastage is not affordable.

Problem Statement: How would you ensure that, in the above situation, you take exactly one tablet from each bottle, at the same time ensuring no wastage of the medicine.


Answer

- Take (1) Pill A from the bottle and add it to the 3 unknown pills. You now have (2) Pill A and (2) Pill B in your pile.
- Take each of the 4 pills and cut them in half.
- For each pill, put one of the halves in a pile on the right and one of the halves in a pile on the left.
- Each pile now contains 2 halves of Pill A and 2 halves of Pill B, which is the same as (1) Pill A and (1) Pill B in each pile.