Let f(n) denote the number of regions for n lines no three of which coincide in one point. This latter condition will guarantee the maximum. Obviously, f(0)=1, f(1)=2, f(2)=4, f(3)=7, etc.
Now, given n-1 lines, there are already f(n-1) regions. With the introduction of the n-th line, imagine the points of intersection of the pre-existing n-1 lines fall on one side of the n-th line. So, on one side of the n-th line -- where the points of intersection lie -- you still have f(n-1) regions, whereas on the other side of the n-th line, you now have n regions. So, for these n lines before us, the total number f(n) of regions must be equal to f(n-1)+n.
So, f(n)=f(n-1)+n. With the initial condition(s) given earlier, this gives us f(n)=1+n(n+1)/2.
we can use induction to prove the same,
Base case:
if n = 1, regions (planes) = 2
Induction Hypothesis:
Addition of a new line adds
---------------------------------------------
|n
---------------------------------------------
regions to the regions formed by previous
---------------------------------------------
|n-1
---------------------------------------------
lines, i.e.
f(n) = n + f(n-1)
Upon simplifying the above, we get f(n) = 1 + n(n+1)/2
"You can punch a hole in an apple using a straw. How do you think that makes your milkshake feel..???" Start Solving It...
Friday, April 29, 2011
Thursday, April 28, 2011
Weighting Puzzles One Side Weighing & two side Weighing
Puzzle 1:
The puzzle is if the shopkeeper can only place the weights in one side of the common balance. For example if shopkeeper has weights 1 and 3 then he can measure 1, 3 and 4 only. Now the question is how many minimum weights and names the weights you will need to measure all weights from 1 to 1000. This is a fairly simple problem and very easy to prove also. Answer for this puzzle is given below.
Solution :
This is simply the numbers 2^0,2^1,2^2 ... that is 1,2,4,8,16... So for making 1000 kg we need up to 1, 2, 4, 8, 16, 32, 64, 128, and 512. Comments your suggestions or other answers.
Puzzle 2:
This is same as the above puzzle with the condition of placing weights on only side of the common balance being removed. You can place weights on both side and you need to measure all weights between 1 and 1000. For example if you have weights 1 and 3,now you can measure 1,3 and 4 like earlier case, and also you can measure 2,by placing 3 on one side and 1 on the side which contain the substance to be weighed. So question again is how many minimum weights and of what denominations you need to measure all weights from 1kg to 1000kg. Answer for this puzzle is given below.
Solution:
For this answer is 3^0, 3^1, 3^2... That is 1,3,9,27,81,243 and 729.
Monday, April 25, 2011
Dropping Eggs from a Building - 100 Story Building Famous Google Puzzle
Source:: Heard From Googlear in Bangalore
You stand before a 100-story building with two eggs. Using only these two eggs, you must figure out the highest floor from which you can drop an egg such that the egg won't break when it hits the ground (we'll call this the "highest safe floor"). Every floor is equally likely to be the highest safe floor, including the top floor, and it's also just as likely that the egg will break from every floor. You can assume that if you drop an egg and it doesn't break, its shell is just as strong as it was before you dropped it.
If you want to minimize the expected number of drops you have to perform, what strategy should you use for picking which floors to drop the eggs from? You should write a program to solve this problem.
Answer: The easiest way to do this would be to start from the first floor and drop the egg. If it doesn’t break, move on to the next floor. If it does break, then we know the maximum floor the egg will survive is 0. If we continue this process, we will easily find out the maximum floors the egg will survive with just one egg. So the maximum number of tries is 100 that is when the egg survives even at the 100th floor.
Can we do better? Of course we can. Let’s start at the second floor. If the egg breaks, then we can use the second egg to go back to the first floor and try again. If it does not break, then we can go ahead and try on the 4th floor (in multiples of 2). If it ever breaks, say at floor x, then we know it survived floor x-2. That leaves us with just floor x-1 to try with the second egg. So what is the maximum number of tries possible? It occurs when the egg survives 98 or 99 floors. It will take 50 tries to reach floor 100 and one more egg to try on the 99th floor so the total is 51 tries. Wow, that is almost half of what we had last time.
Can we do even better? Yes we can (Bob, the builder). What if we try at intervals of 3? Applying the same logic as the previous case, we need a max of 35 tries to find out the information (33 tries to reach 99th floor and 2 more on 97th and 98th floor).
Interval – Maximum tries
1 – 100
2 – 51
3 – 35
4 – 29
5 – 25
6 – 21
7 – 20
8 – 19
9 – 19
10 – 19
11 – 19
12 – 19
13 – 19
14 – 20
15 – 20
16 – 21
So picking any one of the intervals with 19 maximum tries would be fine.
2nd Solution Discussed With Friends You Can Find This @ Many Places
Drop the first egg from 50.If it breaks you can try the same approach for a 50-storey building (1 to 49) and try it from 25th floor. If it did not break try at 75th floor. And use linear search with the remaining portion of storey we need to test. For example if the first egg breaks at 50 we need to try all possibilities from 1 to 49.
Now this looks a feasible solution. In computer student's jargon do a binary search with first egg and linear search with the second one. Best case is log (100) and worst is 50.
Now the optimal solution for the problem is that you figure out that you will eventually end up with a linear search because you have no way of deciding the highest floor with only one egg (If you broke one egg and you have to find the answer among 10 all you can do is start from the lowest to the highest and the worst is the total number of floors). So the whole question grinds up to how to make use of the first egg to reduce the linear testing of the egg.
(For strict computer science students, well this problem can be solved using binary search on the number of drops needed to find the highest floor.)
Now let x be the answer we want, the number of drops required.
So if the first egg breaks maximum we can have x-1 drops and so we must always put the first egg from height x. So we have determined that for a given x we must drop the first ball from x height. And now if the first drop of the first egg doesn’t breaks we can have x-2 drops for the second egg if the first egg breaks in the second drop.
Taking an example, lets say 16 is my answer. That I need 16 drops to find out the answer. Lets see whether we can find out the height in 16 drops. First we drop from height 16,and if it breaks we try all floors from 1 to 15.If the egg don’t break then we have left 15 drops, so we will drop it from 16+15+1 =32nd floor. The reason being if it breaks at 32nd floor we can try all the floors from 17 to 31 in 14 drops (total of 16 drops). Now if it did not break then we have left 13 drops. and we can figure out whether we can find out whether we can figure out the floor in 16 drops.
Lets take the case with 16 as the answer
1 + 15 16 if breaks at 16 checks from 1 to 15 in 15 drops
1 + 14 31 if breaks at 31 checks from 17 to 30 in 14 drops
1 + 13 45 .....
1 + 12 58
1 + 11 70
1 + 10 81
1 + 9 91
1 + 8 100 We can easily do in the end as we have enough drops to accomplish the task
Now finding out the optimal one we can see that we could have done it in either 15 or 14 drops only but how can we find the optimal one. From the above table we can see that the optimal one will be needing 0 linear trials in the last step.
So we could write it as
(1+p) + (1+(p-1))+ (1+(p-2)) + .........+ (1+0) >= 100.
Let 1+p=q which is the answer we are looking for
q (q+1)/2 >=100
Solving for 100 you get q=14.
So the answer is: 14
Drop first orb from floors 14, 27, 39, 50, 60, 69, 77, 84, 90, 95, 99, 100... (i.e. move up 14 then 13, then 12 floors, etc) until it breaks (or doesn't at 100).
3rd way to Approach Suggested by Galye Lakemann
Observation: Regardless of how we drop Egg1, Egg2 must do a linear search. i.e., if Egg1 breaks between floor 10 and 15, we have to check every floor in between with the Egg2
The Approach:
A First Try: Suppose we drop an egg from the 10th floor, then the 20th, …
»»If the first egg breaks on the first drop (Floor 10), then we have at most 10 drops total.
»»If the first egg breaks on the last drop (Floor 100), then we have at most 19 drops total (floors 10, 20, ...,90, 100, then 91 through 99).
»»That’s pretty good, but all we’ve considered is the absolute worst case. We should do some “load balancing” to make those two cases more even.
Goal: Create a system for dropping Egg1 so that the most drops required is consistent, whether Egg1 breaks on the first drop or the last drop.
1. A perfectly load balanced system would be one in which Drops of Egg1 + Drops of Egg2 is always the same, regardless of where Egg1 broke.
2. For that to be the case, since each drop of Egg1 takes one more step, Egg2 is allowed one fewer step.
3. We must, therefore, reduce the number of steps potentially required by Egg2 by one drop each time. For example, if Egg1 is dropped on Floor 20 and then Floor 30, Egg2 is potentially required to take 9 steps. When we drop Egg1 again, we must reduce potential Egg2 steps to only 8. That is, we must drop Egg1 at floor 39.
4. We know, therefore, Egg1 must start at Floor X, then go up by X-1 floors, then X-2, …, until it gets to 100.
5. Solve for X+(X-1)+(X-2)+…+1 = 100. X(X+1)/2 = 100 -> X = 14
We go to Floor 14, then 27, then 39, … This takes 14 steps maximum.
Please feel free to correct or post any comment on the solution or the answer.
4th way to Solve it Purely Computer Science Way
Dynamic Programming
Solution
The key insight to solving this problem is to realize that if you drop and egg and it doesn't break, then you are essentially going to be performing the same problem for a building of a shorter size. For example, if you were to drop an egg from floor 60 and it didn't break, you would then be solving the same problem for floors 61-100, which is like solving it on a 40-story building.
Another important realization is that if your first egg breaks, you must go down to the the highest floor that you know is "safe" (or to the bottom floor if you don't know of any safe floors), and then go up one floor at a time, dropping the egg at each floor until it breaks. This is the only way to ensure that you'll then find the highet safe floor.
Let's generalize these ideas. Assume we decide to drop the first egg from floor k.
* If it breaks, then we'll have to go down to floor 1 and drop the second egg from each floor up to (k-1), or until it breaks. In this case, we expect about k/2 more drops on average, since each of the floors below floor k is is equally likely to be the highest safe floor. In fact, the exact number of drops to expect on average is (1 + 2 + ... + (k-1) + (k-1)) / k. We'll leave it as an exercise to the reader to see why.
* If it doesn't break, then it's as if we're considering the same problem on a building of size (100 - k), where the bottom floor is floor k+1.
* There is some probability of the first egg breaking from floor k. It's actually fairly straightforward to see that this probability is (k/101), because there are 101 possible scenarios (the scenarios in which each floor is the highest safe floor, plus the scenario in which all floors are unsafe). For the general case of an n-floor building, this probability is k/(n+1)
* Thus the probability of the egg not breaking is (1 - k/101), or for the general case, (1 - k/(n+1))
This leads us to define the "Best" formula. The function Best(n), should return the best number of expected drops we can attain for a builing with n stories. We also define the function Best(n,k), which should return the best expected number of drops we can attain for a building with n stories if our first drop is from floor k.
Best(100, k) = 1
+ (probability_of_breaking_from_floor_k * expected_number_of_drops_with_sequential_dropping_starting_at_floor_1)
+ (probablity_of_not_breaking_from_floor_k * Best(100-k))
This formula is based on basic probability theory. The first 1 in the sum is for the current drop. Then we add the expected number of additional drops if the current egg does or does not break, each weighted by the probability of that situation occurring. This gives us the expected total number of drops.
We are looking for Best(100), which we can find by calculating Best(100,k) for all values of k between 1 and 100, and picking the one that returns the minimal value. The value of k associated with this minimal value is the floor we should drop the first egg from.
This formula isn't solveable as is, because it is recursive (it includes a call to the Best() function within itself). But we can see that the recursive call to Best() always uses a number less than 100. This suggests that if we can build up the values for Best() starting at Best(1), then we can use a program to iteratively build up a solution for Best(100).
And that is exactly what we'll do. Below is a program written in the Ruby programming language which solves the problem for 100 floors (though you can change the value), and finishes by printing out the proper floors to drop the egg as the dropping progresses.
Algorithm
PRINT_DEBUG = false
MAX_FLOORS = 100
def probability_of_breaking(cur_floor, num_floors)
return (cur_floor.to_f / (num_floors.to_f + 1.0))
end
def expected_drops_with_final_egg(num_floors_to_check)
if num_floors_to_check == 0
return 0.0
elsif num_floors_to_check == 1
return 1.0
else
numerator = (1..(num_floors_to_check-1)).to_a.inject(0){|p,c| p + c} + (num_floors_to_check * 2)
denominator = num_floors_to_check + 1
return (numerator.to_f / denominator.to_f)
end
end
expected_best = {0 => {:best_num_drops => 0.0, :best_start_floor => 0}}
for num_floors in 1..MAX_FLOORS
cur_best = nil
best_start_floor = nil
puts "======================= #{num_floors} Floors ======================="
for start_floor in 1..num_floors
#if the egg breaks from the current floor, we have to start from the highest floor below the current floor
# where we know the egg won't break from (or floor 1 if we haven't tested from any floors below the current floor)
puts "--- Starting on #{start_floor} of #{num_floors} floors ---" if PRINT_DEBUG
break_probability = probability_of_breaking(start_floor,num_floors)
floors_above = num_floors - start_floor
floors_below = start_floor - 1
expected_floors_if_breaks = expected_drops_with_final_egg(floors_below)
expected_floors_if_does_not_break = expected_best[floors_above][:best_num_drops]
best_expected_drops = 1.0 +
(break_probability * expected_floors_if_breaks) +
((1.0 - break_probability) * expected_floors_if_does_not_break)
puts " probability of breaking: #{break_probability} --- if breaks: #{expected_floors_if_breaks} --- if not: #{expected_floors_if_does_not_break} --- expected drops: #{best_expected_drops}" if PRINT_DEBUG
if cur_best.nil? or best_expected_drops < cur_best cur_best = best_expected_drops best_start_floor = start_floor end end expected_best[num_floors] = {:best_num_drops => cur_best, :best_start_floor => best_start_floor}
end
for k in expected_best.keys.sort
puts "#{k} floors: #{expected_best[k].inspect}"
end
num_floors = MAX_FLOORS
puts "===== For #{num_floors} floors, we expect an average of #{expected_best[num_floors][0]} drops ====="
effective_num_floors = num_floors
base_floor = 0
while true
drop_floor = base_floor + expected_best[effective_num_floors][:best_start_floor]
floors_above = num_floors - drop_floor
effective_floors_below = drop_floor - base_floor - 1
puts "Drop from floor #{drop_floor}"
puts " If it breaks there, you can expect #{expected_drops_with_final_egg(effective_floors_below)} more drops"
effective_num_floors = floors_above
base_floor = drop_floor
break if drop_floor >= num_floors - 1
end
Knight Tour - Yet Another Chess Problem
Source : Heard From My Friend Who Went to Crack Amazon
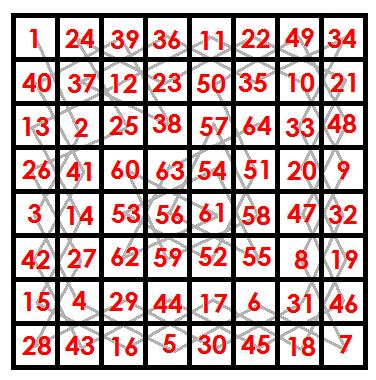
The Knight's Tour is a famous chess problem, in which a knight starts on the top-left square of an ordinary chessboard and then makes 63 moves, landing on every square of the chessboard exactly once (except for the starting square).
Can you complete the Knight's Tour? For a further challenge, can you find a "closed" solution, meaning that the knight can make a 64th move to land back on the starting square (thus making the solution circular)?

Solution
This pictures shows a non-cyclical solution. The strategy is to essentially cover the border (outer 3 rows/columns) first, and then cover the inner part of the board. We'll leave a cyclical solution as a challenge to the reader
More Info
http://en.wikipedia.org/wiki/Knight%27s_tour
The Knight's Tour is a famous chess problem, in which a knight starts on the top-left square of an ordinary chessboard and then makes 63 moves, landing on every square of the chessboard exactly once (except for the starting square).
Can you complete the Knight's Tour? For a further challenge, can you find a "closed" solution, meaning that the knight can make a 64th move to land back on the starting square (thus making the solution circular)?

Solution
This pictures shows a non-cyclical solution. The strategy is to essentially cover the border (outer 3 rows/columns) first, and then cover the inner part of the board. We'll leave a cyclical solution as a challenge to the reader

More Info
http://en.wikipedia.org/wiki/Knight%27s_tour
Subscribe to:
Comments (Atom)